
分析 ①利用双曲线的定义中对a,c的要求即可判断.
②由题意,CP⊥OA,弦OA中点P的轨迹为以OC为直径的圆;
③方程2x2-5x+2=0的两根为:2,$\frac{1}{2}$,故可分别作为椭圆和双曲线的离心率;
④求出双曲线的焦点是(±4,0),椭圆的焦点(±4,0),可得结论.
解答 解:①因为双曲线的定义中要求k<|AB|,故①不正确;
②由题意,CP⊥OA,∴弦OA中点P的轨迹为以OC为直径的圆,故不正确;
③方程2x2-5x+2=0的两根为:2,$\frac{1}{2}$,故可分别作为椭圆和双曲线的离心率,正确;
④∵④中双曲线的焦点是(±4,0),椭圆的焦点(±4,0),∴④正确.
故答案为:③④.
点评 本题考查了椭圆,双曲线的定义,及圆锥曲线的共同特征---离心率,考查了学生的灵活把握定义及基础知识的能了,是个中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
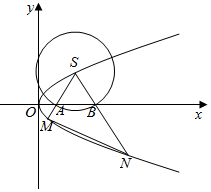 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
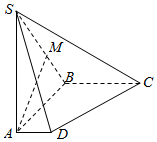 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com