Question

7．设正△ABC的面积为2，边AB，AC的中点分别为D，E，M为线段BE上的动点，则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$²的最小值为$\frac{13\sqrt{3}}{6}$．

Answer 1

分析 建立坐标系，结合三角形的面积可求正三角形的边长，进而可表示B，A，C，E的坐标，然后由M在BE上，结合向量共线可表示M的坐标及已知向量的坐标，代入向量的数量积的坐标表示，结合二次函数的性质即可求解

解答 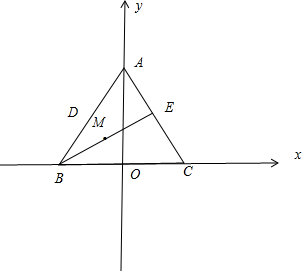解：建立如图所示的坐标系，
设正三角形的边长为a，则$\frac{\sqrt{3}}{4}{a}^{2}$=2，
∴${a}^{2}=\frac{8}{\sqrt{3}}$，
∵B（-$\frac{1}{2}a$，0），C（$\frac{1}{2}a，0$），A（0，$\frac{\sqrt{3}}{2}a$），
∴E（$\frac{a}{4}，\frac{\sqrt{3}a}{4}$），$\overrightarrow{BE}$=$（\frac{3a}{4}，\frac{\sqrt{3}a}{4}）$，$\overrightarrow{BC}=（a，0）$，
设$\overrightarrow{BM}=k\overrightarrow{BE}$=（$\frac{3ka}{4}，\frac{\sqrt{3}ka}{4}$），
∴$\overrightarrow{MC}$=$\overrightarrow{MB}+\overrightarrow{BC}$=（$-\frac{3ka}{4}，-\frac{\sqrt{3}ka}{4}$）+（a，0）=（$\frac{4a-3ka}{4}，-\frac{\sqrt{3}ka}{4}$），
∴则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$²=$-\frac{3ka}{4}×\frac{4a-3ka}{4}+（-\frac{\sqrt{3}ka}{4}）×（-\frac{\sqrt{3}ka}{4}）$+a²
=$\frac{3{a}^{2}}{4}（{k}^{2}-k）+{a}^{2}$，
∵0≤k≤1，
当k=$\frac{1}{2}$时，上式取得最小值$\frac{13\sqrt{3}}{6}$，
故答案为：$\frac{13\sqrt{3}}{6}$．

点评 本题考查了向量的线性运算、数量积运算、二次函数的单调性，考查了推理能力与计算能力，属于中档题．