
ЁОЬтФПЁПЮЊСЫМьВтЩњВњЯпЩЯФГжжСуМўЕФжЪСПЃЌДгВњЦЗжаЫцЛњГщШЁ100ИіСуМўЃЌВтСПЦфГпДчЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЎШєСуМўГпДчТфдкЧјМф![]() жЎФкЃЌдђШЯЮЊИУСуМўКЯИёЃЌЗёдђШЯЮЊВЛКЯИёЃЎЦфжа
жЎФкЃЌдђШЯЮЊИУСуМўКЯИёЃЌЗёдђШЯЮЊВЛКЯИёЃЎЦфжа![]() ЃЌ
ЃЌ![]() ЗжБ№БэЪОбљБОЕФЦНОљжЕКЭБъзМВюЃЌМЦЫуЕУ
ЗжБ№БэЪОбљБОЕФЦНОљжЕКЭБъзМВюЃЌМЦЫуЕУ![]() ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉЃЎ
ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉЃЎ
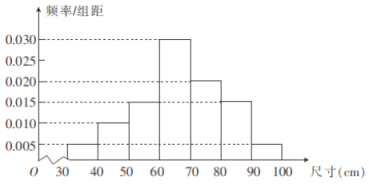
ЃЈ1ЃЉвбжЊвЛИіСуМўЕФГпДчЪЧ![]() ЃЌЪдХаЖЯИУСуМўЪЧЗёКЯИёЃЛ
ЃЌЪдХаЖЯИУСуМўЪЧЗёКЯИёЃЛ
ЃЈ2ЃЉРћгУЗжВуГщбљЕФЗНЗЈДгГпДчдк![]() ЕФбљБОжаГщШЁ6ИіСуМўЃЌдйДгет6ИіСуМўжаЫцЛњГщШЁ2ИіЃЌЧѓет2ИіСуМўжаЧЁга1ИіГпДчаЁгк
ЕФбљБОжаГщШЁ6ИіСуМўЃЌдйДгет6ИіСуМўжаЫцЛњГщШЁ2ИіЃЌЧѓет2ИіСуМўжаЧЁга1ИіГпДчаЁгк![]() ЕФИХТЪЃЎ
ЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉИУСуМўВЛКЯИёЃЎЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЃЌМЦЫуГі![]() ЕФЧјМфЃЌдйХаЖЯ
ЕФЧјМфЃЌдйХаЖЯ![]() ЪЧЗёЪєгкЧјМфФкЃЌМДПЩЕУД№АИЃЛ
ЪЧЗёЪєгкЧјМфФкЃЌМДПЩЕУД№АИЃЛ
ЃЈ2ЃЉМЧет6ИіСуМўБрКХЮЊЃК![]() ЃЌдйСаГіДгет6ИіСуМўжаЫцЛњГщШЁ2ИіЕФЛљБОЪТМўЃЌМЧЪТМў
ЃЌдйСаГіДгет6ИіСуМўжаЫцЛњГщШЁ2ИіЕФЛљБОЪТМўЃЌМЧЪТМў![]() ЮЊЃКЁАбЁГіЕФ2ИіСуМўжаЧЁга1ИіГпДчаЁгк
ЮЊЃКЁАбЁГіЕФ2ИіСуМўжаЧЁга1ИіГпДчаЁгк![]() ЁБЃЌМЦЫуЪТМў
ЁБЃЌМЦЫуЪТМў![]() АќКЌЕФЛљБОЪТМўЃЌРћгУЙХЕфИХаЭМЦЫуИХТЪЃЌМДПЩЕУД№АИЃЛ
АќКЌЕФЛљБОЪТМўЃЌРћгУЙХЕфИХаЭМЦЫуИХТЪЃЌМДПЩЕУД№АИЃЛ
ЃЈ1ЃЉМЧИїзщЕФЦЕТЪЮЊ![]() ЃЌвРЬтвтЕУ
ЃЌвРЬтвтЕУ
![]() ЃЌ
ЃЌ
![]()
Ёр![]()
![]()
Ёр![]()
Жј![]() ЃЌЙЪИУСуМўВЛКЯИёЃЎ
ЃЌЙЪИУСуМўВЛКЯИёЃЎ
ЃЈ2ЃЉМЧЧАШ§зщГщШЁЕФСуМўИіЪ§ЗжБ№ЮЊ![]()
Ёр![]() ЃЌЁр
ЃЌЁр![]()
ЁрГщШЁГіЕФ6ИіСуМўжаГпДчаЁгк![]() ЕФга3ИіЃЎ
ЕФга3ИіЃЎ
МЧет6ИіСуМўБрКХЮЊЃК![]() ЃЈЦфжа
ЃЈЦфжа![]() ЮЊГпДчаЁгк
ЮЊГпДчаЁгк![]() ЕФЃЉ
ЕФЃЉ
МЧЪТМў![]() ЮЊЃКЁАбЁГіЕФ2ИіСуМўжаЧЁга1ИіГпДчаЁгк
ЮЊЃКЁАбЁГіЕФ2ИіСуМўжаЧЁга1ИіГпДчаЁгк![]() ЁБ
ЁБ
ЁрДгет6ИіСуМўжаЫцЛњГщШЁ2ИіЕФЛљБОЪТМўгаЃК
![]()
![]() ЙВ15ИіЃЎ
ЙВ15ИіЃЎ
дђЪТМў![]() АќКЌЕФЛљБОЪТМўгаЃК
АќКЌЕФЛљБОЪТМўгаЃК
![]() ЙВ9Иі
ЙВ9Иі
Ёр![]()
Ёрет2ИіСуМўжаЧЁга1ИіГпДчаЁгк![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБШ§Ртжљ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() жаЕуЃЌ
жаЕуЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕу.
ЩЯЕФвЛИіЖЏЕу.
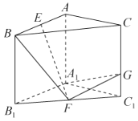
ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЪБЃЌжЄУїЃК
ЪБЃЌжЄУїЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ.
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ.
ЃЈ1ЃЉШєКЏЪ§![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЕФаБТЪЮЊ
ДІЕФЧаЯпЕФаБТЪЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЬжТлКЏЪ§
ЪБЃЌЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ3ЃЉШєЙигк![]() ЕФВЛЕШЪН
ЕФВЛЕШЪН![]() дкЧјМф
дкЧјМф![]() ЩЯКуГЩСЂЃЌЧѓЪЕЪ§
ЩЯКуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЯЪРМЭФЉКгФЯГіЭСЕФвдКзЕФГпЙЧЃЈГсЙЧЃЉжЦГЩЕФЁАЙЧЕбЁБЃЈЭМ1ЃЉЃЌГфЗжеЙЪОСЫЮвЙњЙХДњИпГЌЕФвєТЩвеЪѕМАЯШНјЕФЪ§бЇЫЎЦНЃЌвВгЁжЄСЫЮвЙњЙХДњвєТЩгыРњЗЈЕФУмЧаСЊЯЕ.ЭМ2ЮЊЙЧЕбВтСПЁАДКЃЈЧяЃЉЗжЁБЃЌЁАЯФЃЈЖЌЃЉжСЁБЕФЪОвтЭМЃЌЭМ3ЪЧФГЙЧЕбЕФВПЗжВтСПЪ§ОнЃЈЙЧЕбЕФЭфЧњКіТдВЛМЦЃЉЃЌЯФжСЃЈЛђЖЌжСЃЉШеЙтЃЈЕБШее§ЮчЬЋбєЙтЯпЃЉгыДКЧяЗжШеЙтЃЈЕБШее§ЮчЬЋбєЙтЯпЃЉЕФМаНЧЕШгкЛЦГрНЛНЧ.

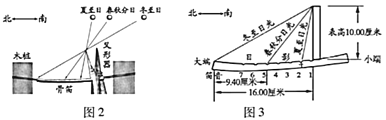
гЩРњЗЈРэТлжЊЃЌЛЦГрНЛНЧНќ1ЭђФъГжајМѕаЁЃЌЦфе§ЧажЕМАЖдгІЕФФъДњШчЯТБэЃК
ЛЦГрНЛНЧ |
|
|
|
|
|
е§ЧажЕ | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
ФъДњ | ЙЋдЊдЊФъ | ЙЋдЊЧА2000Фъ | ЙЋдЊЧА4000Фъ | ЙЋдЊЧА6000Фъ | ЙЋдЊЧА8000Фъ |
ИљОнвдЩЯаХЯЂЃЌЭЈЙ§МЦЫуЛЦГрНЛНЧЃЌПЩЙРМЦИУЙЧЕбЕФДѓжТФъДњЪЧ( )
A.ЙЋдЊЧА2000ФъЕНЙЋдЊдЊФъB.ЙЋдЊЧА4000ФъЕНЙЋдЊЧА2000Фъ
C.ЙЋдЊЧА6000ФъЕНЙЋдЊЧА4000ФъD.дчгкЙЋдЊЧА6000Фъ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНЬхABCDЉA1B1C1D1жаЃЌAA1ЃН8ЃЌABЃН3ЃЌADЃН8ЃЌЕуMЪЧРтADЕФжаЕуЃЌЕуNЪЧРтAA1ЕФжаЕуЃЌPЪЧВрУцЫФБпаЮADD1A1ФквЛЖЏЕуЃЈКЌБпНчЃЉЃЌШєC1PЁЮЦНУцCMNЃЌдђЯпЖЮC1PГЄЖШЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
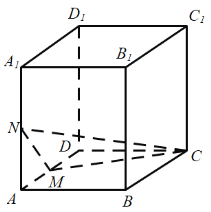
A.![]() B.[4ЃЌ5]C.[3ЃЌ5]D.
B.[4ЃЌ5]C.[3ЃЌ5]D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇМЦЛЎНЈЩшжСЩй3ИіЃЌжСЖр5ИіЯрЭЌЕФЩњВњЯпГЕМфЃЌвдНтОіБОЕиЧјЙЋУёЖдЬиЙЉЩЬЦЗ![]() ЕФЮДРДашЧѓЃЎОЙ§ЖдЯШЦкбљБОЕФПЦбЇадЕїВщЯдЪОЃЌБОЕиЧјУПИідТЖдЩЬЦЗ
ЕФЮДРДашЧѓЃЎОЙ§ЖдЯШЦкбљБОЕФПЦбЇадЕїВщЯдЪОЃЌБОЕиЧјУПИідТЖдЩЬЦЗ![]() ЕФдТашЧѓСПОљдк50ЭђМўМАвдЩЯЃЌЦфжаашЧѓСПдк50~ 100ЭђМўЕФЦЕТЪЮЊ0.5ЃЌашЧѓСПдк100~200ЭђМўЕФЦЕТЪЮЊ0.3ЃЌВЛЕЭгк200ЭђМўЕФЦЕТЪЮЊ0.2ЃЎгУЕїВщбљБОРДЙРМЦзмЬхЃЌЦЕТЪзїЮЊЯргІЖЮЕФИХТЪЃЌВЂМйЩшБОЕиЧјдкИїИідТЖдБОЬиЙЉЩЬЦЗ
ЕФдТашЧѓСПОљдк50ЭђМўМАвдЩЯЃЌЦфжаашЧѓСПдк50~ 100ЭђМўЕФЦЕТЪЮЊ0.5ЃЌашЧѓСПдк100~200ЭђМўЕФЦЕТЪЮЊ0.3ЃЌВЛЕЭгк200ЭђМўЕФЦЕТЪЮЊ0.2ЃЎгУЕїВщбљБОРДЙРМЦзмЬхЃЌЦЕТЪзїЮЊЯргІЖЮЕФИХТЪЃЌВЂМйЩшБОЕиЧјдкИїИідТЖдБОЬиЙЉЩЬЦЗ![]() ЕФашЧѓЯрЛЅЖРСЂЃЎ
ЕФашЧѓЯрЛЅЖРСЂЃЎ
ЃЈ1ЃЉЧѓдкЮДРДФГСЌај4ИідТжаЃЌБОЕиЧјжСЩйга2ИідТЖдЩЬЦЗ![]() ЕФдТашЧѓСПЕЭгк100ЭђМўЕФИХТЪЃЎ
ЕФдТашЧѓСПЕЭгк100ЭђМўЕФИХТЪЃЎ
ЃЈ2ЃЉИУЙЄГЇЯЃЭћОЁПЩФмдкЩњВњЯпГЕМфНЈГЩКѓЃЌГЕМфФме§ГЃЩњВњдЫааЃЌЕЋУПдТзюЖрПЩе§ГЃЩњВњЕФГЕМфЪ§ЪмЩЬЦЗ![]() ЕФашЧѓСП
ЕФашЧѓСП![]() ЕФЯожЦЃЌВЂгаШчЯТЙиЯЕЃК
ЕФЯожЦЃЌВЂгаШчЯТЙиЯЕЃК
ЩЬЦЗ |
|
|
|
ГЕМфзюЖре§ГЃдЫааИіЪ§ | 3 | 4 | 5 |
ШєвЛИіГЕМфе§ГЃдЫааЃЌдђИУГЕМфдТОЛРћШѓЮЊ1500ЭђдЊЃЌЖјвЛИіГЕМфЮДе§ГЃЩњВњЃЌдђИУГЕМфЩњВњЯпЕФдТЮЌЛЄЗбЃЈЕЅЮЛЃКЭђдЊЃЉгыдТашЧѓСПгаШчЯТЙиЯЕЃК
ЩЬЦЗ |
|
|
ЮДе§ГЃЩњВњЕФвЛИіГЕМфЕФдТЮЌЛЄЗбЃЈЭђдЊЃЉ | 500 | 600 |
ЪдЗжЮіВЂЛиД№ИУЙЄГЇгІНЈЩшЩњВњЯпГЕМфЖрЩйИіЃПЪЙЕУЩЬЦЗ![]() ЕФдТРћШѓЮЊзюДѓЃЎ
ЕФдТРћШѓЮЊзюДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌвддЕу
ЃЌвддЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎШєНЋЧњЯп
ЃЎШєНЋЧњЯп![]() ЩЯЕФЫљгаЕуЕФКсзјБъЫѕаЁЕНдРДЕФвЛАыЃЌзнзјБъЩьГЄЕНдРДЕФ
ЩЯЕФЫљгаЕуЕФКсзјБъЫѕаЁЕНдРДЕФвЛАыЃЌзнзјБъЩьГЄЕНдРДЕФ![]() БЖЃЌЕУЧњЯп
БЖЃЌЕУЧњЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉаДГіжБЯп![]() КЭЧњЯп
КЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌ жБЯп
ЃЌ жБЯп![]() гыЧњЯп
гыЧњЯп![]() ЕФСНИіНЛЕуЗжБ№ЮЊ
ЕФСНИіНЛЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃИпжаШ§ИіФъМЖЙВга4000ШЫЃЌЮЊСЫСЫНтИїФъМЖбЇжмФЉдкМвЕФбЇЯАЧщПіЃЌЯжЭЈЙ§ЗжВуГщбљЕФЗНЗЈЛёЕУЯрЙиЪ§ОнШчЯТЃЈЕЅЮЛЃКаЁЪБЃЉЃЌЦфжаИпвЛбЇЩњжмФЉЕФЦНОљбЇЯАЪБМфМЧЮЊ![]() .
.
ИпвЛЃК14 15 15.5 16.5 17 17 18 19
ИпЖўЃК15 16 16 16 17 17 18.5
ИпШ§ЃК16 17 18 21.5 24
(1)ЧѓУПИіФъМЖЕФбЇЩњШЫЪ§ЃЛ
(2)ДгИпШ§БЛГщВщЕФЭЌбЇжаЫцЛњГщШЁ2ШЫЃЌЧѓ2ШЫбЇЯАЪБМфОљГЌЙ§![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com