
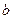 和
和 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程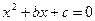 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。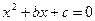 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;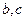 中至少有一个为3,求方程
中至少有一个为3,求方程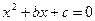 有实根的概率。
有实根的概率。 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源:不详 题型:单选题
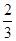 ,向右移动的概率为
,向右移动的概率为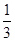 ,则电子兔移动五次后位于点
,则电子兔移动五次后位于点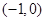 的概率是( )
的概率是( )A.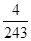 | B.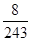 | C.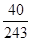 | D.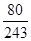 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的概率分布列及数学期望。
的概率分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 和
和 ,则( )
,则( )A. = = | B. > > | C. < < | D.以上三种情况都有可能 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
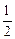 ,各次投篮相互独立,令此选手投篮n次的命中率为
,各次投篮相互独立,令此选手投篮n次的命中率为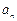 (
(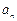 为进球数与n之比),则事件“
为进球数与n之比),则事件“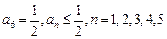 ”发生的概率为( )
”发生的概率为( )A.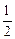 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com