
 的概率分布列及数学期望。
的概率分布列及数学期望。 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是 ,甲、乙、丙全部做错的概率是
,甲、乙、丙全部做错的概率是 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与乙队的每个队员各握手一次 (同队的队员之间不握手),从这n2次的握手中任意取两次.记
与乙队的每个队员各握手一次 (同队的队员之间不握手),从这n2次的握手中任意取两次.记 ,求n的最小值.
,求n的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
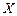 的概率分布列和数学期望.
的概率分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
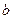 和
和 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程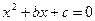 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。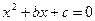 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;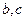 中至少有一个为3,求方程
中至少有一个为3,求方程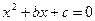 有实根的概率。
有实根的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
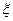 表示,椐统计,随机变量
表示,椐统计,随机变量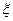 的概率分布如下:
的概率分布如下: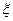 | 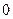 | 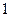 | 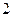 | 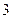 |
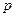 | 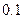 | 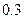 | 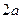 | 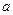 |
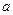 的值和
的值和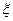 的数学期望;
的数学期望;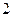 次的概率。
次的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
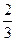 ,各次过关与否互不影响,且此人不放弃所有机会。
,各次过关与否互不影响,且此人不放弃所有机会。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com