
已知圆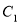 的圆心在坐标原点
的圆心在坐标原点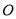 ,且恰好与直线
,且恰好与直线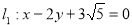 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,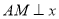 轴于点
轴于点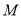 ,且动点
,且动点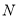 满足
满足 ,设动点
,设动点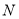 的轨迹为曲线
的轨迹为曲线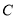
(1)求曲线C的方程,
(2)直线l与直线l,垂直且与曲线C交于B、D两点,求△OBD面积的最大值.
(1) 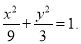 ;(2)
;(2) 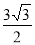
【解析】
试题分析:(1)此题考察轨迹方程,考察代入法的习题,根据圆心到直线的距离等于半径,可以求出圆的半径,即知道圆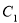 的方程
的方程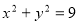 ,设动点
,设动点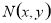 ,
, ,
,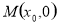 ,利用公式
,利用公式 ,写出向量相等的坐标表示,利用
,写出向量相等的坐标表示,利用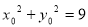 ,代入,得到关于
,代入,得到关于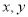 的方程;
的方程;
(2)利用直线方程与椭圆方程联立,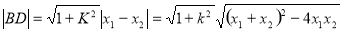 和点到直线的距离公式,得出面积,并求出最大值.
和点到直线的距离公式,得出面积,并求出最大值.
(1)设动点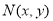 ,
, 因为
因为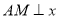 轴于
轴于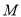 ,所以
,所以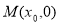 ,
,
设圆 的方程为
的方程为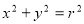 ,由题意得
,由题意得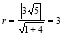 , 所以圆
, 所以圆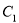 的程为
的程为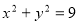 .
.
由题意, 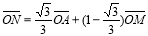 ,所以
,所以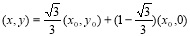 ,
,
所以 即
即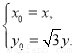
将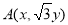 代入圆
代入圆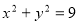 ,得动点
,得动点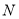 的轨迹方程
的轨迹方程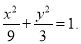
(2)由题意可设直线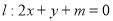 ,设直线
,设直线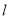 与椭圆
与椭圆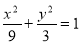 交于
交于 ,
,
联立方程 得
得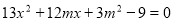 ,
,
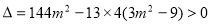 ,解得
,解得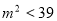 ,
, 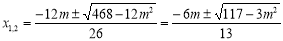 ,
,
又因为点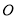 到直线
到直线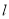 的距离
的距离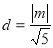 ,
,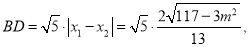


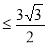 .(当且仅当
.(当且仅当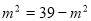 即
即 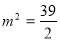 时取到最大值)
时取到最大值)  面积的最大值为
面积的最大值为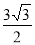 .
.
考点:1.代入法求轨迹方程;2.直线方程与圆锥曲线联立;3.弦长公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年浙江省六市六校联盟高考模拟理科数学试卷(解析版) 题型:解答题
如图,已知圆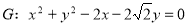 ,经过椭圆
,经过椭圆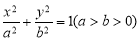 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点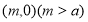 倾斜角为
倾斜角为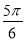 的直线
的直线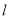 交椭圆于C,D两点,
交椭圆于C,D两点,
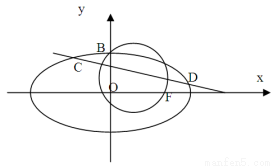
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)理科数学试卷(解析版) 题型:选择题
若两非零向量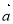 与
与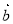 的夹角为
的夹角为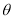 ,定义向量运算
,定义向量运算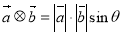 ,已知向量
,已知向量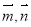 满足
满足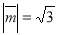 ,
,
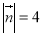 ,
, ,则
,则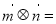 ( )
( )
A.2 B.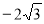 C.
C.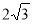 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)理科数学试卷(解析版) 题型:选择题
复数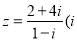 为虚数单位)在复平面内对应点的坐标是( )
为虚数单位)在复平面内对应点的坐标是( )
A.(3,3) B.(一1,3) C(3,一1) D.(2,4)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)文科数学试卷(解析版) 题型:填空题
等边三角形ABC的边长为2,将它沿高AD翻折,使点B与点C问的距离为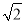 ,此时四面体
,此时四面体
ABCD外接球体积为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)文科数学试卷(解析版) 题型:选择题
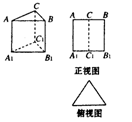
如右图,三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥底面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )
A.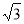
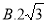 C.4 D.
C.4 D.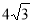
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省郑州市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
某工厂为了对新研发的一种产品进行合理定价,交该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 5 | 6 | 7 | 8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为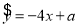 ,若在这些样本点中任取一点,则它在回归直线左下方的概率为
,若在这些样本点中任取一点,则它在回归直线左下方的概率为
A.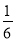 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:解答题
如图,四边形ABCD是边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点C、F,连接CF并延长交AB于点E.
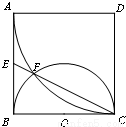
(Ⅰ)求证:E是AB的中点。
(Ⅱ)求线段BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com