
设函数f(x)=ax+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 .
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
若函数f (x) (x∈R)是偶函数,函数g (x) (x∈R)是奇函数,则
(A)函数f [g(x)]是奇函数 (B)函数g [f (x)]是奇函数
(C)函数f (x)+g(x)是奇函数 (D)函数f (x) g(x)是奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= ex,a,b
ex,a,b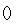 R,且a>0.
R,且a>0.
(1)若a=2,b=1,求函数f(x)的极值;
(2)设g(x)=a(x-1)ex-f(x).
① 当a=1时,对任意x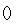 (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;
② 设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求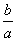 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)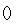 Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
第十八届省运会将于2014年9月在徐州市举办.为营造优美的环境,举办方决定在某“葫芦”形花坛中建喷泉.如图,该花坛的边界是两个半径为10米的圆弧围成,两圆心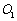 、
、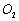 之间的距离为
之间的距离为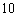 米.
米.
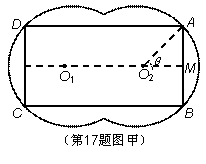
( 1)如图甲,在花坛中建矩形喷泉,四个顶点
1)如图甲,在花坛中建矩形喷泉,四个顶点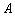 ,
,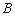 ,
,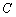 ,
,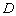 均在圆弧上,
均在圆弧上,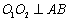 于点
于点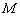 .设
.设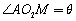 ,求矩形的宽
,求矩形的宽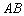 为多少时,可使喷泉
为多少时,可使喷泉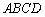 的面积最大;
的面积最大;
(2)如图乙,在花坛中间铺设一条宽为2米的观赏长廊以作休闲之用,则矩形喷泉变为两个全等的等腰三角形,其中 ,
,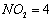 米.若
米.若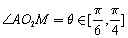 ,求喷泉的面积的取值范围.
,求喷泉的面积的取值范围.
 | |||
 | |||
查看答案和解析>>
科目:高中数学 来源: 题型:
以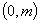 间的整数
间的整数 为分子,以
为分子,以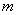 为分母组成分数集合
为分母组成分数集合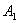 ,其所有元素和为
,其所有元素和为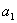 ;以
;以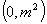 间的整数
间的整数 为分子,以
为分子,以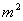 为分母组成不属于集合
为分母组成不属于集合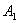 的分数集合
的分数集合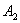 ,其所有元素和为
,其所有元素和为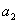 ;……,依次类推以
;……,依次类推以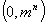 间的整数
间的整数 为分子,以
为分子,以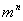 为分母组成不属于
为分母组成不属于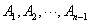 的分数集合
的分数集合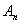 ,其所有元素和为
,其所有元素和为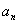 ;则
;则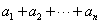 =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com