
设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)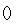 Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
解:(1)因为f(1)f(4)=f(4)+f(4),所以5 f(1)=10,则f(1)=2.
因为f(n)是单调增函数,
所以2=f(1)<f(2)<f(3)<f(4)=5.
因为f(n)∈Z,所以f(2)=3,f(3)=4.
(2)解:由(1)可猜想f (n)=n+1.
证明:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z,
所以f (n+1)≥f (n)+1.
首先证明:f (n)≥n+1.
因为f (1)=2,所以n=1时,命题成立.
假设n=k(k≥1)时命题成立,即f(k)≥k+1.
则f(k+1)≥f (k)+1≥k+2,即n=k+1时,命题也成立.
综上,f (n)≥n+1.
由已知可得f (2)f (n)=f (2n)+f (n+1),而f(2)=3,f (2n)≥2n+1,
所以3 f (n)≥f (n+1)+2n+1,即f(n+1)≤3 f (n)-2n-1.
下面证明:f (n)=n+1.
因为f (1)=2,所以n=1时,命题成立.
假设n=k(k≥1)时命题成立,即f(k)=k+1,
则f(k+1)≤3f (k)-2k-1=3(k+1)-2k-1=k+2,
又f(k+1)≥k+2,所以f(k+1)=k+2.
即n=k+1时,命题也成立.
所以f (n)=n+1
解法二:由f(1)=2,f(2)=3,f(3)=4,f(4)=5,猜想f(n)=n+1.
下面用数学归纳法证明:
①当n=1,2,3,4时,命题成立.
②假设当n≤k (k≥4)时,命题成立,下面讨论n=k+1的情形.
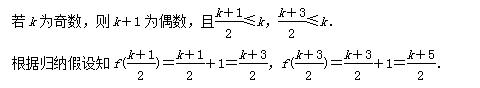
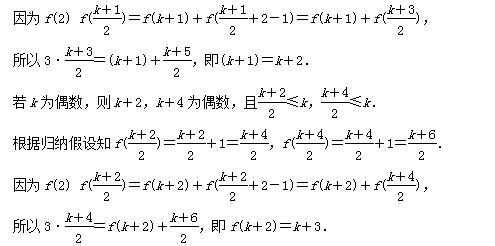
又k+1=f(k)<f(k+1)<f(k+2)=k+3.
所以f(k+1)=k+2
因此不论k的奇偶性如何,总有f(k+1)=k+2,即n=k+1时,命题也成立
于是对一切n∈N*,f(n)=n+1.
解法三:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z,
所以f (n+1)≥f (n)+1,又f(1)=2,所以f (n)≥n+1
由已知可得:f (2)f (n)=f (2n)+f (n+1)
而f(2)=3,f (2n)≥2n+1
所以3 f (n)≥f (n+1)+2n+1,即:f(n+1)≤3 f (n)-2n-1
或者f(n+1)-n-2≤3(f (n)-n-1)
所以有f(n+1)-n-2≤3(f (n)-n-1)
≤32(f (n-1)-n)
≤33(f (n-2)-n+1)
……
≤3n(f (1)-2)=0
于是f(n+1)≤n+2
又f (n+1)≥n+2
所以f(n+1)=n+2,又f(1)=2
所以f(n)=n+1


科目:高中数学 来源: 题型:
设函数f(x)=ax+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
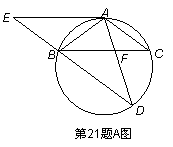
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与
DB的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ACBE为平行四边形;
(2)若AE=6,BD=5,求线段CF的长.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com