
分析 由题意可得圆心C(2,0),推导出点P到圆上的点的最小距离应小于或等于半径r=2.设点P的坐标为(m,m+3),则$\sqrt{(m-2)^{2}+(m+3{-0)}^{2}}$-2≤2,由此能求出点P的横坐标的取值范围.
解答 解:由题意可得圆心C(2,0),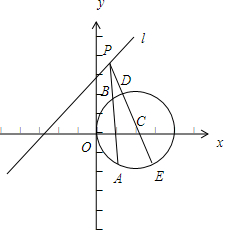
∵点P在直线l:y=x+3上,圆C上存在两点A、B使得$\overrightarrow{PA}$=3$\overrightarrow{PB}$,
如图,|AB|=2|PB|,|CD|=|CE|=r=2,
∴点P到圆上的点的最小距离|PD|应小于或等于半径r=2.
设点P的坐标为(m,m+3),
则$\sqrt{(m-2)^{2}+(m+3{-0)}^{2}}$-2≤2,
化简可得2m2+2m-3≤0,解得$\frac{-1-\sqrt{7}}{2}$≤m≤$\frac{-1+\sqrt{7}}{2}$,
∴点P的横坐标的取值范围是:$[{\frac{{-1-\sqrt{7}}}{2},\frac{{-1+\sqrt{7}}}{2}}]$
故答案为:$[{\frac{{-1-\sqrt{7}}}{2},\frac{{-1+\sqrt{7}}}{2}}]$.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,判断点P到圆上的点的最小距离应小于或等于半径,是解题的关键,体现了转化的数学思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2ln2 | B. | -ln2 | C. | ln2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知$|{\overrightarrow{OA}}|=1$,$|{\overrightarrow{OB}}|=\sqrt{3}$,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为90°,点C在AB上,且∠AOC=30°.设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),求$\frac{m}{n}$的值.
已知$|{\overrightarrow{OA}}|=1$,$|{\overrightarrow{OB}}|=\sqrt{3}$,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为90°,点C在AB上,且∠AOC=30°.设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),求$\frac{m}{n}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com