Question

【题目】在平面直角坐标系xOy中，椭圆C： + =1（a＞b＞0）的离心率e= ，且点P（2，1）在椭圆C上． （Ⅰ）求椭圆C的方程；
（Ⅱ）若点A、B都在椭圆C上，且AB中点M在线段OP（不包括端点）上．求△AOB面积的最大值．

Answer 1

【答案】解：（Ⅰ）由题意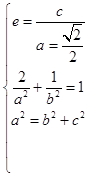得： ，解得 ， ∴椭圆C的方程为 ；
（Ⅱ）设A（x1 ， y1），B（x2 ， y2），M（x0 ， y0），直线AB的斜率为k，
则 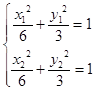，两式作差可得 ，得 ，
又直线OP： ，M在线段OP上，
∴ ，解得k=﹣1．
设直线AB的方程为y=﹣x+m，m∈（0，3），
联立 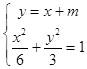，得3x2﹣4mx+2m2﹣6=0，
△=16m2﹣12（2m2﹣6）=72﹣8m2＞0，得﹣3＜m＜3．
．
∴|AB|= ，原点到直线的距离d= ，
∴ ．
当且仅当 ∈（0，3）时，等号成立．
∴△OAB面积的最大值
【解析】（Ⅰ）由题意列出关于a，b，c的方程组，求解方程组可得a，b的值，则椭圆方程可求；（Ⅱ）利用“点差法”求出A，B所在直线的斜率，设出直线方程，与椭圆方程联立，由弦长公式求得弦长，再由点到直线的距离公式求出原点到直线AB的距离，代入三角形面积公式，利用基本不等式求得最值．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．