
【题目】已知长方体![]() 中,
中, ![]() 为
为![]() 的中点,如图所示.
的中点,如图所示.
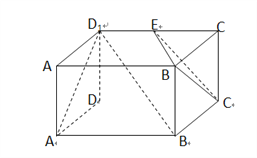
(1) 证明: ![]() 平面
平面![]() ;
;
(2) 求平面![]() 与平面
与平面![]() 所成锐二面角的大小的余弦值.
所成锐二面角的大小的余弦值.
【答案】(1)见解析(2) ![]() .
.
【解析】试题分析:
(1)连接![]() 交
交![]() 于
于![]() ,易知
,易知![]() ,可得
,可得![]() 平面
平面![]() ;
;
(2) 平面![]() 即是平面
即是平面![]() ,过平面
,过平面![]() 上点
上点![]() 作
作![]() 的垂线于
的垂线于![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线于
的垂线于![]() ,连接
,连接![]() ,证明
,证明![]() 即是平面
即是平面![]() 与平面
与平面![]() 所成锐二面角的平面角,求解易得结果;
所成锐二面角的平面角,求解易得结果;
向量法:(1) 以![]() 所在直线分别为
所在直线分别为![]() 轴,以
轴,以![]() 为坐标原点,建立空间直角坐标系,求出平面
为坐标原点,建立空间直角坐标系,求出平面![]() 的一个法向量
的一个法向量![]() ,证明
,证明![]() ,则可得结论;
,则可得结论;
(2)求出平面![]() 的一个法向量
的一个法向量![]() ,再利用向量的夹角公式求解即可.
,再利用向量的夹角公式求解即可.
试题解析:
(1)连接![]() 交
交![]() 于
于![]() ,因为在长方体
,因为在长方体![]() 中,所以
中,所以
![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点
的中点
所以在![]() 中
中![]() 是中位线,所以
是中位线,所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)因为在长方体![]() 中,所以
中,所以![]() ,
,
平面![]() 即是平面
即是平面![]() ,过平面
,过平面![]() 上
上
点![]() 作
作![]() 的垂线于
的垂线于![]() ,如平面图①,
,如平面图①,
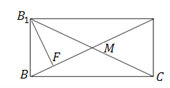
平面图①
因为在长方体![]() 中,
中, ![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() 于
于![]() .
.
过点![]() 作直线
作直线![]() 的垂线于
的垂线于![]() ,如平面图②,
,如平面图②,
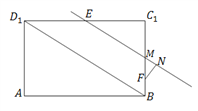
平面图②
连接![]() ,由三垂线定理可知,
,由三垂线定理可知, ![]() .
.
由二面角的平面角定义可知,在![]() 中,
中,
![]() 即是平面
即是平面![]() 与平面
与平面![]() 所成锐二面角的平面角.
所成锐二面角的平面角.
因长方体![]() 中,
中, ![]() ,在平面图①中,
,在平面图①中,
![]() ,
,
![]() ,
,
在平面图②中,由![]() 相似
相似![]() 可知
可知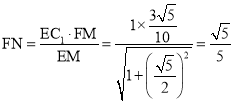 ,
,
所以![]() =2,
=2,
![]() ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的大小的余弦值为
所成锐二面角的大小的余弦值为![]() .
.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 满足
满足![]() ,
, ![]()
(Ⅰ)若![]() ,求
,求![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列,求
成等比数列,求![]() 的值;
的值;
(Ⅲ)是否存在![]() ,使得
,使得![]() 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin ωx-cos ωx(ω>0)的最小正周期为π.
(1)求函数y=f(x)图象的对称轴方程;
(2)讨论函数f(x)在![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
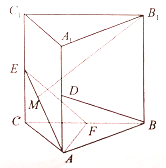
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且
,且![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上的任意一点,求直线
上的任意一点,求直线![]() 与平面
与平面![]() 所成角正弦的最大值.
所成角正弦的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)已知当![]() (其中
(其中![]() 是自然对数的底数)时,在
是自然对数的底数)时,在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,对任意
时,对任意![]() ,有
,有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() , 直线
, 直线![]() 过点
过点![]() .
.
(Ⅰ)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() , 求直线
, 求直线![]() 的斜率;
的斜率;
(Ⅱ)设![]() 为抛物线上两点, 且
为抛物线上两点, 且![]() 不与
不与![]() 轴垂直, 若线段
轴垂直, 若线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() , 求证: 线段
, 求证: 线段![]() 中点的横坐标为定值.
中点的横坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
支持 | 保留 | 不支持 | |
30岁以下 | 900 | 120 | 280 |
30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com