
【题目】《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.下图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体
,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体![]() 中,鳖臑有( )个.
中,鳖臑有( )个.
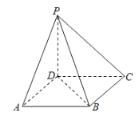
A.0B.1C.2D.3
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的已套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
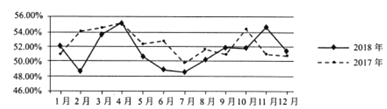
A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 这两年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与x轴交于A,B两点,点Q的坐标为
与x轴交于A,B两点,点Q的坐标为![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,说明理由;
,如果存在求出b值;如果不存在,说明理由;
(2)过A,B,Q三点的圆面积最小时,求圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
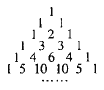
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
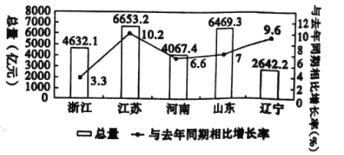
A. 2017年第一季度GDP增速由高到低排位第5的是浙江省.
B. 与去年同期相比,2017年第一季度的GDP总量实现了增长.
C. 去年同期河南省的GDP总量不超过4000亿元 .
D. 2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com