
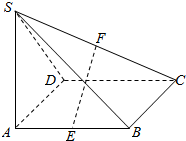
 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.分析 (Ⅰ)要证EF∥面SAD,只要证明EF平行于面内的一条直线;
(Ⅱ)关键是分别求出平面SBC,SCD的面积;首先要判断它们各自的形状.
解答 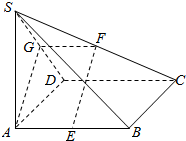 (Ⅰ)证明:因为E是AB中点,F是SC的中点,过F作FG∥CD,
(Ⅰ)证明:因为E是AB中点,F是SC的中点,过F作FG∥CD,
则G是SD的中点,(1分)
又因为$AE\underline{\underline{∥}}\frac{1}{2}DC$,所以$FG\underline{\underline{∥}}AE$.(2分)
所以四边形AEFG是平行四边形,所以EF∥AG,(3分)
又因为EF?面SAD,AG?面SAD,所以EF∥平面SAD.(4分)
(Ⅱ)解:因为SA⊥平面ABCD,底面ABCD是正方形,
所以BC⊥AB,BC⊥SA
且AB∩SA=A,所以BC⊥平面SAB.(8分)
又因为SB?平面SAB,所以BC⊥SB.所以△SBC是直角三角形.(9分)
SB=$\sqrt{S{A}^{2}+A{B}^{2}}$=2$\sqrt{2}$,所以${S_{Rt△SBC}}=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$.(10分)
同理可得${S_{Rt△SDC}}=2\sqrt{2}$.(11分)又S△SAD=S△SAB=2,
所以四棱锥S-ABCD的侧面积是4+4$\sqrt{2}$.(12分)
点评 本题考查了空间线面平行、线面垂直的判定定理和性质定理的运用;关键是将线面关系转化为线线关系.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
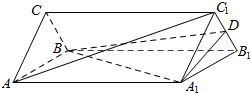 如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.
如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com