
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
分析 (Ⅰ)由表中的数据分别计算$\overline{x}$,$\overline{y}$,$\sum_{i=1}^{4}$xiyi,$\sum_{i=1}^{4}$${{x}_{i}}^{2}$,$\stackrel{∧}{b}$,$\stackrel{∧}{a}$,即可写出线性回归方程;
(Ⅱ)由线性回归方程,计算x=10时,$\stackrel{∧}{y}$的值即可.
解答 解:(Ⅰ)由表中的数据得$\overline{x}=\frac{2+3+5+6}{4}=4$,(1分)
$\overline{y}=\frac{7+8+9+12}{4}=9$,(2分)
$\sum_{i=1}^4{{x_i}{y_i}}=2×7+3×8+5×9+6×12=155$,(3分)
$\sum_{i=1}^4{x_i^2}={2^2}+{3^2}+{5^2}+{6^2}=74$,(4分)
$\hat b=\frac{{\sum_{i=1}^4{{x_i}{y_i}}-4\bar x\bar y}}{{\sum_{i=1}^4{x_i^2-4{{\bar x}^2}}}}=\frac{155-4×4×9}{{74-4×{4^2}}}=\frac{11}{10}=1.1$,(6分)
$\hat a=\bar y-\hat b\overline{x}=9-1.1×4=4.6$,(7分)
所以所求线性回归方程为$\hat y=1.1x+4.6$;(8分)
(Ⅱ)由(1)得,当x=10时,$\hat y=1.1×10+4.6=15.6$,
即产量为10千件时,成本约为15.6万元. (10分)
点评 本题考查了求线性回归方程的应用问题,也考查了利用线性回归方程预测生产问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
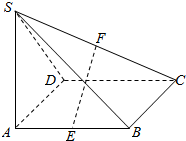 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
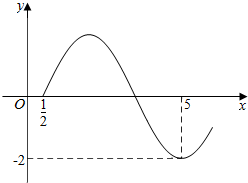 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com