
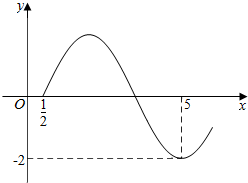
 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.分析 (Ⅰ) 求出函数的周期,求出ω,利用特殊点,求解φ,即可求函数的解析式;
(Ⅱ) 借助函数的图象之间求解当x∈[-5,-2]时,函数f(x)的最大值和最小值.
解答  解:(Ⅰ)由图象可知,函数的周期为T=6,
解:(Ⅰ)由图象可知,函数的周期为T=6,
$ω=\frac{2π}{6}=\frac{π}{3}$.…(2分)
又f(x)的图象过点$({\frac{1}{2},0})$,所以$2sin({\frac{π}{3}×\frac{1}{2}+φ})=0$
所以$\frac{π}{3}×\frac{1}{2}+φ=2kπ$,即$φ=2kπ-\frac{π}{6},k∈Z$,又因为$-\frac{π}{2}<φ<0$,所以$φ=-\frac{π}{6}$,…(4分)
故所求函数的解析式是$f(x)=2sin({\frac{π}{3}x-\frac{π}{6}})$.…(5分)
(Ⅱ) 因为函数$f(x)=2sin({\frac{π}{3}x-\frac{π}{6}})$的周期是T=6,所以求x∈[-5,-2]时函数f(x)的最大值和最小值就是转化为求函数在区间[1,4]上的最大值和最小值.…(8分)
由图象可知,当x=2时,函数的最大值是$f(2)=2sin({\frac{π}{3}×2-\frac{π}{6}})=2$;…(10分)
当x=4时,函数的最小值是$f(4)=2sin({\frac{π}{3}×4-\frac{π}{6}})=-1$.…(12分).
点评 本题考查三角函数的解析式的求法,函数的最值以及函数的图象的应用,本题也可以直接求函数$f(x)=2sin({\frac{π}{3}x-\frac{π}{6}})$在区间[-5,-2]上的最大值和最小值.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a,-b,-c) | B. | (-a,b,-c) | C. | (-a,-b,c) | D. | (-a,-b,-c) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
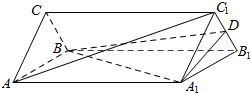 如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.
如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com