
【题目】已如椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点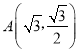 在E上.
在E上.
(1)求E的方程:
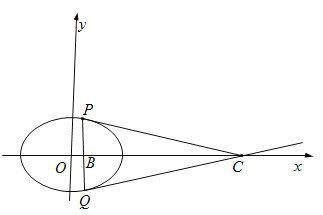
(2)斜率不为0的直线l经过点![]() ,且与E交于P,Q两点,试问:是否存在定点C,使得
,且与E交于P,Q两点,试问:是否存在定点C,使得![]() ?若存在,求C的坐标:若不存在,请说明理由
?若存在,求C的坐标:若不存在,请说明理由
【答案】(1)![]() (2)存在x轴上的定点
(2)存在x轴上的定点![]() ,使得
,使得![]()
【解析】
(1)根据椭圆离心率和过的点,得到关于![]() ,
,![]() 的方程组,解得
的方程组,解得![]() ,
,![]() 的值,从而得到椭圆的方程;(2)设存在定点
的值,从而得到椭圆的方程;(2)设存在定点![]() ,对称性可知设
,对称性可知设![]() ,根据
,根据![]() ,得到
,得到![]() ,即得
,即得![]() ,直线
,直线![]() 的方程为:
的方程为:![]() 与椭圆联立,得到
与椭圆联立,得到![]() ,
,![]() ,从而得到
,从而得到![]() 和
和![]() 的关系式,根据对
的关系式,根据对![]() 恒成立,从而得到
恒成立,从而得到![]() 的值.
的值.
(1)因为椭圆E的离心率![]() ,所以
,所以![]() ①,
①,
点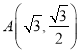 在椭圆上,所以
在椭圆上,所以![]() ②,
②,
由①②解得![]() ,
,![]() .
.
故E的方程为![]() .
.
(2)假设存在定点![]() ,使得
,使得![]() .
.
由对称性可知,点![]() 必在
必在![]() 轴上,故可设
轴上,故可设![]() .
.
因为![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 的倾斜角互补,因此
的倾斜角互补,因此![]() .
.
设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
由 消去
消去![]() ,得
,得![]() ,
,
![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() .
.
整理得![]() ,
,
所以![]() ,即
,即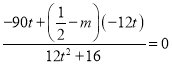 .
.
所以![]() ,即
,即![]() ,对
,对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,所以
恒成立,所以![]() .
.
所以存在定点![]() ,使得
,使得![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
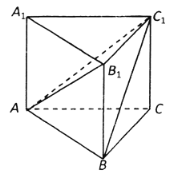
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,与抛物线
,与抛物线![]() 有公共焦点
有公共焦点![]() .
.
(1)求椭圆C1与抛物线![]() 的方程;
的方程;
(2)已知直线![]() 是圆
是圆![]() 的一条切线,与椭圆C1交于
的一条切线,与椭圆C1交于![]() 两点,若直线
两点,若直线![]() 斜率存在且不为
斜率存在且不为![]() ,在椭圆C1上存在点
,在椭圆C1上存在点![]() ,使
,使![]() ,其中
,其中![]() 为坐标原点,求实数λ的取值范围.
为坐标原点,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年电商“双十一”大战即将开始.某电商为了尽快占领市场,抢占今年“双十一”的先机,对成都地区年龄在15到75岁的人群“是否网上购物”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用网上购物的人数如下所示:(年龄单位:岁)
年龄段 |
|
|
|
|
|
|
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
购物人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | 总计 | |
使用网上购物 | |||
不使用网上购物 | |||
总计 |
(2)若从年龄在![]() 的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
的样本中随机选取2人进行座谈,求选中的2人中恰好有1人“使用网上购物”的概率.
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com