
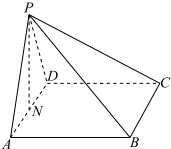
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥AB,N是棱AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥AB,N是棱AD的中点.分析 (Ⅰ)证明AB⊥平面PAD,再证明:平面PAB⊥平面PAD;
(Ⅱ)证明PN⊥AD,AB⊥PN,利用线面垂直的判定定理证明:PN⊥平面ABCD;
(Ⅲ)在棱BC上存在点E,使得BN∥平面DEP,此时E为BC的中点,证明BN∥DE即可.
解答 (Ⅰ)证明:在矩形ABCD中,AB⊥AD.…(1分)
又∵AB⊥PA且PA∩AD=A,
∴AB⊥平面PAD.…(3分)
又∵AB?平面PAB,
∴平面PAB⊥平面PAD.…(4分)
(Ⅱ)证明:在△PAD中,PA=PD,N是棱AD的中点,∴PN⊥AD.…(5分)
由(Ⅰ)知AB⊥平面PAD,∴AB⊥PN.…(7分)
又∵AB∩AD=A,∴PN⊥平面ABCD.…(8分)
(Ⅲ)解:在棱BC上存在点E,使得BN∥平面DEP,此时E为BC的中点.…(10分)
证明如下:
取BC中点E,连接PE,DE.…(11分)
在矩形ABCD中,ND∥BE,ND=BE,
所以四边形BNDE为平行四边形,∴BN∥DE.…(13分)
又∵BN?平面DEP,DE?平面DEP,所以BN∥平面DEP.…(14分)
点评 本题考查线面垂面面垂直的判定,考查线面平行的判定,考查学生分析解决问题的能力,正确运用定理是关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
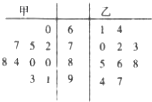 某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<c<a | B. | c<a<b | C. | c<b<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com