
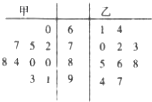
 某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.分析 (Ⅰ)由平均数公式分别求得$\overline{{x}_{甲}}$和$\overline{{x}_{乙}}$,分别与原数据对比,即可求得m和n的值,并比较大小;
(Ⅱ)由题意可知:X可取0,1,2,求出相应概率,可得X的分布列,从而可求数学期望E(X).
解答 解:(Ⅰ)$\overline{{x}_{甲}}$=$\frac{1}{10}$(60+72+75+77+80+80+84+88+91+93)=80,
甲班“口语王”人数为m=4,
$\overline{{x}_{乙}}$=$\frac{1}{10}$(61+64+70+72+73+85+86+88+97+94)=79,
乙班“口语王”人数为n=5,
∴m<n,
(Ⅱ)由题意可知:X可取0,1,2,
P(X=0)=$\frac{{C}_{4}^{0}{C}_{5}^{2}}{{C}_{9}^{2}}$=$\frac{5}{18}$,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{5}^{1}}{{C}_{9}^{2}}$=$\frac{5}{9}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{5}^{0}}{{C}_{9}^{2}}$=$\frac{1}{6}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{5}{18}$ | $\frac{5}{9}$ | $\frac{1}{6}$ |
点评 本题考查概率与统计,考查茎叶图的运用,随机变量的分布列与期望,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{|{a+b}|}}{2}$≥$\sqrt{|{ab}|}$ | B. | $\frac{b}{a}$+$\frac{a}{b}$≥2 | C. | $\frac{{{a^2}+{b^2}}}{2}$≥(${\frac{a+b}{2}}$)2 | D. | (a+b)($\frac{1}{a}$+$\frac{1}{b}$)≥4(a+b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
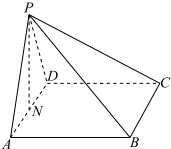 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥AB,N是棱AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥AB,N是棱AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com