
| A. | $\frac{{|{a+b}|}}{2}$≥$\sqrt{|{ab}|}$ | B. | $\frac{b}{a}$+$\frac{a}{b}$≥2 | C. | $\frac{{{a^2}+{b^2}}}{2}$≥(${\frac{a+b}{2}}$)2 | D. | (a+b)($\frac{1}{a}$+$\frac{1}{b}$)≥4(a+b) |
分析 直接利用基本不等式的性质考查各选项即可得到答案.
解答 解:对于A:$\frac{|a+b|}{2}≥\sqrt{ab}$,当ab同号的时,不等式成立,当ab异号时,不成立,故A不对;
对于B:$\frac{a}{b}+\frac{b}{a}≥2$,当ab同号的时,不等式成立,当ab异号时,$-(\frac{a}{b}+\frac{b}{a})≥2\sqrt{\frac{a}{b}\frac{b}{a}}=2$,那么$\frac{a}{b}+\frac{b}{a}≤-2$,故B不对;
对于C:∵$\frac{{a}^{2}+{b}^{2}}{2}-\frac{(a+b)^{2}}{4}=\frac{{a}^{2}+{b}^{2}-2ab}{4}=\frac{(a-{b}^{2})}{4}$≥0,则有:$\frac{{a}^{2}+{b}^{2}}{2}≥(\frac{a+b}{2})^{2}$,故C对;
对于D:$(a+b)(\frac{1}{a+b})=2+\frac{a}{b}+\frac{b}{a}$,当ab同号的时,$\frac{a}{b}+\frac{b}{a}≥2$,原不等式成立,当ab异号时,$-(\frac{a}{b}+\frac{b}{a})≥2\sqrt{\frac{a}{b}\frac{b}{a}}=2$,那么$\frac{a}{b}+\frac{b}{a}≤-2$,原不等式不成立,故D不对;
故选:C.
点评 本题考查了基本不等式的性质的变形与运用.比较综合性.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{e},+∞)$ | B. | $(-\frac{1}{{\sqrt{e}}},\sqrt{e})$ | C. | $(-\sqrt{e},\frac{1}{{\sqrt{e}}})$ | D. | $(-\frac{1}{{\sqrt{e}}},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | $\frac{32}{3}$π | C. | 4$\sqrt{3}$π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取5人,则其中成绩在区间[142,148]上的运动员人数是( )
在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取5人,则其中成绩在区间[142,148]上的运动员人数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
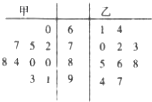 某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<c<a | B. | c<a<b | C. | c<b<a | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com