
【题目】设函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() 在
在![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,求证:
,求证: ![]() 有唯一零点的充要条件是
有唯一零点的充要条件是![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)讨论两种情况,当![]() 时,不是单调函数,当
时,不是单调函数,当![]() 时,由
时,由![]() ,
, ![]() 在
在![]() 为单调递增函数,从而可得结果;(2) 当
为单调递增函数,从而可得结果;(2) 当![]() 时,研究函数的单调性可得函数
时,研究函数的单调性可得函数![]() 有唯一零点,若函数
有唯一零点,若函数![]() 有唯一零点,用反证法可证明只有
有唯一零点,用反证法可证明只有![]() 合题意.
合题意.
试题解析:(1)![]()
当a>0时,由![]() 得
得![]()
当![]() 时,
时, ![]() ,
, ![]() 为单调增函数;
为单调增函数;
当![]() 时,
时, ![]() ,
, ![]() 为单调减函数,
为单调减函数,
所以![]() 在
在![]() 上不为单调函数
上不为单调函数
当![]() 时,由
时,由![]() ,
, ![]() 在
在![]() 为单调递增函数,
为单调递增函数,
所以实数![]() 得取值范围是
得取值范围是![]() 。
。
(2)充分性:当![]() 时,
时, ![]() ,
, ![]()
令![]() 得
得![]()
当![]() 时,
时, ![]() ,
, ![]() 为单调增函数,所以
为单调增函数,所以![]()
当![]() 时,
时, ![]() ,
, ![]() 为单调减函数,所以
为单调减函数,所以![]()
所以函数![]() 有唯一零点
有唯一零点![]()
必要性:设函数![]() 有唯一零点
有唯一零点![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为![]() ,由(1)知,当且仅当
,由(1)知,当且仅当![]() 时,
时,![]() 取得最小值
取得最小值
![]()
记![]() ,所以
,所以![]()
令![]() 得
得![]()
当![]() 时,
时, ![]() ,
, ![]() 为单调减函数,
为单调减函数, ![]()
即![]()
因为![]() ,且
,且![]() ,
,
所以![]() 在
在![]() 内有零点,与题意相矛盾。
内有零点,与题意相矛盾。
当![]() 时,同理有
时,同理有![]()
因为![]() ,存在-
,存在- ![]() ,有
,有![]()
所以![]() 在
在![]() 内有零点,与题意相矛盾。
内有零点,与题意相矛盾。
故![]()
综上, ![]() 有唯一零点的充要条件是
有唯一零点的充要条件是![]() 。
。


科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的月固定成本为10(万元),每生产![]() 件,需另投入成本为
件,需另投入成本为![]() (万元).当月产量不足30件时,
(万元).当月产量不足30件时, ![]() (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, ![]() (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)当月产量为多少件时,该厂所获月利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个命题:
①在回归分析中, ![]() 可以用来刻画回归效果,
可以用来刻画回归效果, ![]() 的值越大,模型的拟合效果越好;
的值越大,模型的拟合效果越好;
②在独立性检验中,随机变量![]() 的值越大,说明两个分类变量有关系的可能性越大;
的值越大,说明两个分类变量有关系的可能性越大;
③在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位;
平均增加1个单位;
④两个随机变量相关性越弱,则相关系数的绝对值越接近于1;
其中真命题是:
A. ①④ B. ②④ C. ①② D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,
,![]() ,
,![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和4名
和4名![]() ,
, ![]() ,
, ![]() ,
, ![]() ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(Ⅰ)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的频率.
的频率.
(Ⅱ)用![]() 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养鸡场为检验某种药物预防某种疾病的效果,取100只鸡进行对比试验,得到如下列联表(表中部分数据丢失, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 表示丢失的数据):
表示丢失的数据):
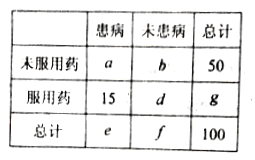
工作人员记得![]() .
.
(1)求出列联表中数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)能否在犯错误的概率不超过0.005的前提下认为药物有效?
参考公式: 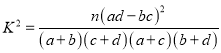 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名学生参加某电视台举办的国学知识竞赛,在竞赛中,他们的出场顺序被组委会随机安排.
(1)求甲、乙、丙三名学生在这次国学知识竞赛中,甲被安排第一个出场的概率;
(2)求甲、乙、丙三名学生在这次国学知识竞赛中,甲比乙出场的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com