
分析 (1)a、b为正实数,且a+b=2$\sqrt{2}$ab.可得a+b=2$\sqrt{2}$ab≥2$\sqrt{ab}$,解得ab≥$\frac{1}{2}$,可得2(a2+b2)≥(a+b)2=8a2b2,即可得出.
(2)由a、b为正实数,且a+b=2$\sqrt{2}$ab.可得(a-b)2=(a+b)2-4ab=8a2b2-4ab≥4(ab)3,化简即可得出.
解答 解:(1)∵a、b为正实数,且a+b=2$\sqrt{2}$ab.
∴a+b=2$\sqrt{2}$ab≥2$\sqrt{ab}$,解得ab≥$\frac{1}{2}$,当且仅当a=b=$\frac{\sqrt{2}}{2}$时取等号.
∴2(a2+b2)≥(a+b)2=8a2b2≥$8×(\frac{1}{2})^{2}$=2,化为a2+b2≥1,当且仅当a=b=$\frac{\sqrt{2}}{2}$时取等号.
∴a2+b2的最小值是1.
(2)∵a、b为正实数,且a+b=2$\sqrt{2}$ab.
∴(a-b)2=(a+b)2-4ab=8a2b2-4ab≥4(ab)3,
化为:(ab-1)2≤0,∴ab=1.
点评 本题考查了基本不等式的性质、不等式的解法、变形能力,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 10 | C. | 4 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
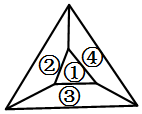
 如图,用4种不同的颜色对图中的5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻区域不能涂相同颜色,则不同的涂色方案有( )种.
如图,用4种不同的颜色对图中的5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻区域不能涂相同颜色,则不同的涂色方案有( )种.| A. | 60 | B. | 72 | C. | 84 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写了一封信,信中提到了他认为应该很简单的一道小谜题.他一直尝试着给一张英国各郡的地图着色,在这个过程中,他发现使用四中颜色就可以实现他的目的,即使相邻的两个郡具有不同的颜色.“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”他写道.
《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写了一封信,信中提到了他认为应该很简单的一道小谜题.他一直尝试着给一张英国各郡的地图着色,在这个过程中,他发现使用四中颜色就可以实现他的目的,即使相邻的两个郡具有不同的颜色.“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”他写道.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (23,12) | B. | (7,0) | C. | (-7,0) | D. | (-23,-12) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com