
已知点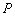 是圆
是圆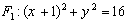 上任意一点(
上任意一点(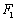 是圆心),点
是圆心),点 与点
与点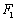 关于原点对称.线段
关于原点对称.线段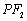 的中垂线
的中垂线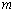 分别与
分别与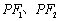 交于
交于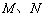 两点.
两点.
(I)求点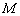 的轨迹
的轨迹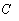 的方程;
的方程;
(Ⅱ)直线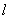 经过F2,与抛物线y2=4x交于A1,A2两点,与
经过F2,与抛物线y2=4x交于A1,A2两点,与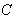 交于B1,B2两点.当以B1B2为直径的圆经过F1时,求|A1A2|.
交于B1,B2两点.当以B1B2为直径的圆经过F1时,求|A1A2|.
解:(I)由题意得,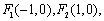 圆
圆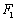 的半径为
的半径为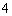 ,且
,且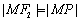
从而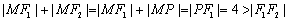 ………… 2分
………… 2分
∴ 点M的轨迹是以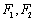 为焦点的椭圆, ………… 4分
为焦点的椭圆, ………… 4分
其中长轴 ,得到
,得到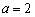 ,焦距
,焦距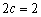 ,
,
则短半轴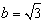
椭圆方程为: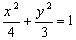 ………… 5分
………… 5分
(Ⅱ)当直线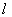 与x轴垂直时,B1(1,
与x轴垂直时,B1(1,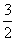 ),B2(1,-
),B2(1,-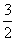 ),又F1(-1,0),
),又F1(-1,0),
此时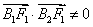 ,所以以B1B2为直径的圆不经过F1.不满足条件.……………(6分)
,所以以B1B2为直径的圆不经过F1.不满足条件.……………(6分)
当直线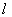 不与x轴垂直时,设L:y=k(x-1)
不与x轴垂直时,设L:y=k(x-1)
由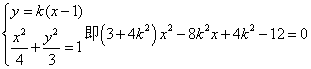
因为焦点在椭圆内部,所以恒有两个交点.
设B1(x1,y1),B2(x2,y2),则
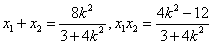
因为以B1B2为直径的圆经过F1,所以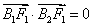 ,又F1(-1,0)
,又F1(-1,0)
所以(-1-x1)(-1-x2)+y1y2=0,即(1+k2)x1x2+(1-k2)(x1+x2)+1+k2=0
所以解得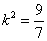 ……………(8分)
……………(8分)
由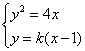 得k2x2-(2k2+4)x+k2=0
得k2x2-(2k2+4)x+k2=0
因为直线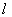 与抛物线有两个交点,所以
与抛物线有两个交点,所以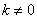
设A1(x3,y3) ,A2(x4,y4),则
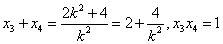
所以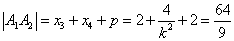 . …………(12分)
. …………(12分)


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
B.命题“∃x0∈R,x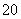 +x0-1<0”的否定是“∀x∈R,x2+x-1>0”
+x0-1<0”的否定是“∀x∈R,x2+x-1>0”
C.命题“若x=y,则sin x=sin y”的逆否命题为假命题
D.若“p或q”为真命题,则p,q中至少有一个为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A.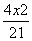 -
-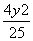 =1 B.
=1 B.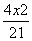 +
+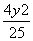 =1 C.
=1 C.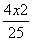 -
-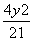 =1 D.
=1 D.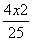 +
+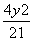 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
把下面在平面内成立的结论类比地推广到空间,结论仍然正确的是____ ____.(填序号)
____.(填序号)
①如果一条直线与两条平行线中的一条相交,则也与另一条相交;
②如果一条直线与两条平行线中的一条垂直,则也与另一条垂直;
③如果两条直线同时与第三条直线相交,则这两条直线相交或平行;
④如果两条直线同时与第三条直线垂直,则这两条直线平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com