
【题目】某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
.统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)该天型超市负责人决定利用分层抽样的方法从前2组中随机抽出5天数据分析日纯利润较少的原因,并从这5天数据中再抽出其中2天数据进行深入分析,求这2天的数据恰好来自不同组的概率;
(3)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为![]() 万元,当
万元,当![]() 时,奖励每位员工40元/天;当
时,奖励每位员工40元/天;当![]() 时,奖励每位员工80元/天;当
时,奖励每位员工80元/天;当![]() 时,奖励每位员工120元/天;
时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
【答案】(1)平均数为6.85万元,中位数为![]() 万元;(2)
万元;(2)![]() ;(3)方案一
;(3)方案一
【解析】
(1)直接计算平均值和中位数得到答案.
(2)记来自于![]() 的1天为
的1天为![]() ,来自于
,来自于![]() 的4天分别为
的4天分别为![]() ,
,![]() ,
,![]() ,
,![]() ,列出所有情况,计算满足条件的情况,得到概率.
,列出所有情况,计算满足条件的情况,得到概率.
(3)根据计算两种方案的奖金的平均值,比较大小得到答案.
(1)这100天该大型超市日纯利润的平均数为:
![]() (万元).
(万元).
前2组频率之和为![]() ,前3组频率之和为
,前3组频率之和为![]() ,
,
故中位数位于第3组.
设中位数为![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
即这100天该大型超市日纯利润的中位数为![]() 万元.
万元.
(2)由分层抽样知识可知,所抽取的5天数据中,来自于![]() ,
,![]() 这2组的天数分别为1,4.记来自于
这2组的天数分别为1,4.记来自于![]() 的1天为
的1天为![]() ,来自于
,来自于![]() 的4天分别为
的4天分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则从中抽取2天的数据的所有可能结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种,
,共10种,
其中这2天的数据来自不同组的有:![]() ,
,![]() ,
,![]() ,
,![]() ,共4种.
,共4种.
故所求的概率为![]() .
.
(3)设选择方案一时小张每天的奖金为![]() 元,
元,
则![]() 的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
所以获得奖金的平均数![]() (元).
(元).
设选择方案二时小张每天的奖金为![]() 元,
元,
则获得奖金的平均数![]() (元).
(元).
因为![]() ,所以从统计角度看,小张选择方案一更有利.
,所以从统计角度看,小张选择方案一更有利.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90°,求证:AQ∥BM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.若圆C上存在点M,使MA=2MO,则圆心C的横坐标a的取值范围是( )
A.![]() B.[0,1]
B.[0,1]
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市抽查了100天该超市的日纯利润数据,并将日纯利润数据分成以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计结果如下表所示:
,统计结果如下表所示:
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率,解决下列问题:
(1)从该大型超市近几年的销售记录中抽出5天,求其中日纯利润在区间![]() 内的天数不少于2的概率;
内的天数不少于2的概率;
(2)该超市经理由频数分布表可以认为,该大型超市每天的纯利润![]() 服从正态分布
服从正态分布![]() ,其中,
,其中,![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).
(每组数据取区间的中点值).
①试利用该正态分布,估计该大型超市1000天内日纯利润在区间![]() 内的天数(精确到个位);
内的天数(精确到个位);
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案:
方案一:直接发放奖金,日纯利润低于![]() 时每名员工发放奖金70元,日纯利润不低于
时每名员工发放奖金70元,日纯利润不低于![]() 时每名员工发放奖金90元;
时每名员工发放奖金90元;
方案二:利用抽奖的方式获得奖金,其中日纯利润不低于![]() 时每位员工均有两次抽奖机会,日纯利润低于
时每位员工均有两次抽奖机会,日纯利润低于![]() 时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工,则从数学期望的角度看,小张选择哪种奖励方案更有利?
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇为了打赢脱贫攻坚战,决定盘活贫困村的各项经济发展要素,实施了产业、创业、就业“三业并举”工程.在实施过程中,引导某贫困村农户因地制宜开展种植某经济作物.该类经济作物的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,其质量指标的等级划分如下表1:
,其质量指标的等级划分如下表1:
表1
质量指标值 | 产品等级 |
| 优秀品 |
| 良好品 |
| 合格品 |
| 不合格品 |
为了解该类经济作物在当地的种植效益,当地引种了甲、乙两个品种.并随机抽取了甲、乙两个品种的各![]() 件产品,测量了每件产品的质量指标值,得到下面产品质量指标值频率分布直方图(图1和图2).
件产品,测量了每件产品的质量指标值,得到下面产品质量指标值频率分布直方图(图1和图2).
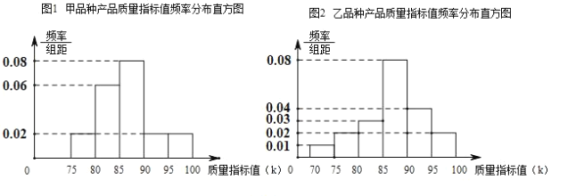
(1)若将频率视为概率,从乙品种产品中有放回地随机抽取![]() 件,记“抽出乙品种产品中至少
件,记“抽出乙品种产品中至少![]() 件良好品或以上”为事件
件良好品或以上”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;(结果保留小数点后
;(结果保留小数点后![]() 位)(参考数值:
位)(参考数值:![]() ,
,![]() )
)
(2)若甲、乙两个品种的销售利润率![]() 与质量指标值
与质量指标值![]() 满足表2
满足表2
表2
质量指标值 |
|
|
|
|
销售利润率 |
|
|
|
|
其中![]() ,试分析,从长期来看,种植甲、乙哪个品种的平均利润率较大?
,试分析,从长期来看,种植甲、乙哪个品种的平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a为常数)有两个极值点.
(a为常数)有两个极值点.
(1)求实数a的取值范围;
(2)设f(x)的两个极值点分别为x1,x2,若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
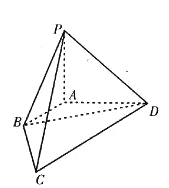
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com