
����Ŀ��ij����Ϊ�˴�Ӯ��ƶ����ս�������̻�ƶ����ĸ���÷�չҪ�أ�ʵʩ�˲�ҵ����ҵ����ҵ����ҵ���١�����.��ʵʩ�����У�����ijƶ����ũ��������˿�չ��ֲij��������.���ྭ�������������������ָ��ֵ������������ָ��ֵԽ���������Խ�ã���������ָ��ֵΪ![]() ��������ָ��ĵȼ��������±�1��
��������ָ��ĵȼ��������±�1��
��1
����ָ��ֵ | ��Ʒ�ȼ� |
| ����Ʒ |
| ����Ʒ |
| �ϸ�Ʒ |
| ���ϸ�Ʒ |
Ϊ�˽���ྭ�������ڵ��ص���ֲЧ�棬���������˼ס�������Ʒ��.�������ȡ�˼ס�������Ʒ�ֵĸ�![]() ����Ʒ��������ÿ����Ʒ������ָ��ֵ���õ������Ʒ����ָ��ֵƵ�ʷֲ�ֱ��ͼ��ͼ1��ͼ2��.
����Ʒ��������ÿ����Ʒ������ָ��ֵ���õ������Ʒ����ָ��ֵƵ�ʷֲ�ֱ��ͼ��ͼ1��ͼ2��.
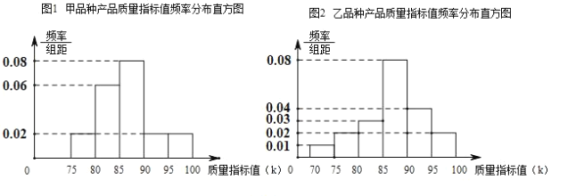
��1������Ƶ����Ϊ���ʣ�����Ʒ�ֲ�Ʒ���зŻص������ȡ![]() �����ǡ������Ʒ�ֲ�Ʒ������
�����ǡ������Ʒ�ֲ�Ʒ������![]() ������Ʒ�����ϡ�Ϊ�¼�
������Ʒ�����ϡ�Ϊ�¼�![]() �����¼�
�����¼�![]() �����ĸ���
�����ĸ���![]() ��(�������С�����
��(�������С�����![]() λ)(�ο���ֵ��
λ)(�ο���ֵ��![]() ��
��![]() )
)
��2�����ס�������Ʒ�ֵ�����������![]() ������ָ��ֵ
������ָ��ֵ![]() �����2
�����2
��2
����ָ��ֵ |
|
|
|
|
���������� |
|
|
|
|
����![]() ���Է������ӳ�����������ֲ�ס����ĸ�Ʒ�ֵ�ƽ�������ʽϴ�
���Է������ӳ�����������ֲ�ס����ĸ�Ʒ�ֵ�ƽ�������ʽϴ�
���𰸡���1��![]() ��2����ֲ��Ʒ�ֵ�ƽ�������ʽϴ�
��2����ֲ��Ʒ�ֵ�ƽ�������ʽϴ�
��������
��1�������������Ʒ�ֲ�Ʒ�г�ȡһ��Ϊ����Ʒ�����ϡ��ĸ��ʣ������ö���ֲ��ĸ��ʹ�ʽ����¼�![]() �Ķ����¼������ĸ��ʣ����������
�Ķ����¼������ĸ��ʣ����������
��2���ֱ�������ֲ�ס������ֲ�Ʒ�������ʵ���ѧ�������Ƚ����ǵĴ�С���ɵó���
��1���衰����Ʒ�ֲ�Ʒ�г�ȡһ��Ϊ����Ʒ�����ϡ��ĸ���Ϊ![]() ��
��
�����Ƶ�ʷֲ�ֱ��ͼ�ɵ�![]() ��
��
��![]()
��2����Ƶ�ʷֲ�ֱ��ͼ�ɵã���Ʒ�ֲ�Ʒ�������ʵķֲ���Ϊ
|
|
|
|
|
|
|
|
![]()
��Ʒ�ֲ�Ʒ�������ʵķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
![]()
![]()
����![]() ������
������![]() ����
����![]() .
.
����ֲ��Ʒ�ֵ�ƽ�������ʽϴ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˵����Уѧ���Ա������ߵĹ�ϵ���Ը�У1000��ѧ������![]() �ı������г������飬�õ�����Ƶ���ֲ������£�
�ı������г������飬�õ�����Ƶ���ֲ������£�
��������Ƶ�ʷֲ���
�������� ����λ�����ף� |
|
|
|
|
|
|
Ƶ�� | 7 | 10 | 19 | 18 | 4 | 2 |
Ů������Ƶ���ֲ���
Ů������ ����λ�����ף� |
|
|
|
|
|
|
Ƶ�� | 3 | 10 | 15 | 6 | 3 | 3 |
��1��������1000��ѧ����Ů����������
��2��������1000��ѧ����������![]() �ĸ��ʣ�
�ĸ��ʣ�
��3���������У���������![]() ��Ů������ȡ3��Ů�����е��飬��
��Ů������ȡ3��Ů�����е��飬��![]() ��ʾ��ѡ3��ѧ����������
��ʾ��ѡ3��ѧ����������![]() ����������
����������![]() �ķֲ��к���ѧ����.�����ߵ�λ�����ף�
�ķֲ��к���ѧ����.�����ߵ�λ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������aΪ���㳣����
������aΪ���㳣����
![]() ����
����![]() �ļ�ֵ���������˵�����ɣ�
�ļ�ֵ���������˵�����ɣ�
![]() ��
��![]() ��
��![]() ֤����
֤����![]() ������
������![]() �����ҽ���1����㣻
�����ҽ���1����㣻![]() ��
��![]() Ϊ
Ϊ![]() �ļ�ֵ�㣬
�ļ�ֵ�㣬![]() Ϊ
Ϊ![]() �������
�������![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͳ��г����100��ó��е��մ��������ݣ����ֳ������¼��飨��λ����Ԫ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .ͳ�ƽ�����±���ʾ��ͳ�Ʊ���ÿ��С��ȡ�м�ֵ��Ϊ�������ݵ����ֵ����
.ͳ�ƽ�����±���ʾ��ͳ�Ʊ���ÿ��С��ȡ�м�ֵ��Ϊ�������ݵ����ֵ����
��� |
|
|
|
|
|
|
Ƶ�� | 5 | 20 | 30 | 30 | 10 | 5 |
��1������100��ô��ͳ����մ������ƽ��������λ����
��2�������ͳ��и����˾������÷ֲ�����ķ�����ǰ2����������5�����ݷ����մ�������ٵ�ԭ������5���������ٳ������2�����ݽ����������������2�������ǡ�����Բ�ͬ��ĸ��ʣ�
��3���������������ֲ���������ֲ�������������⣺�ô��ͳ����ܾ�������ÿ��Ĵ������Ա���ƶ������ֽ���������
����һ�����մ�����Ϊ![]() ��Ԫ����
��Ԫ����![]() ʱ������ÿλԱ��40Ԫ/�죻��
ʱ������ÿλԱ��40Ԫ/�죻��![]() ʱ������ÿλԱ��80Ԫ/�죻��
ʱ������ÿλԱ��80Ԫ/�죻��![]() ʱ������ÿλԱ��120Ԫ/�죻
ʱ������ÿλԱ��120Ԫ/�죻
���������մ��������������λ��ʱÿ��Ա�����Ž���50Ԫ/�죬�մ�������������λ��ʱÿ��Ա������80Ԫ����/�죻
��С��ǡ��Ϊ�ô��ͳ��е�һλԱ�������ͳ�ƽǶȿ���С��ѡ�����ֽ���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У���ֱ֪��l����P��2��2��.������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ������cos2����4cos����0.
��1����C��ֱ�����귽�̣�
��2����l��C����A��B���㣬�� �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�����Կ��贫ͳ�Ļ��ε�̬�ȣ��������������ȡ��![]() λ��������˽⣬����֧�ֿ�չ��ռ
λ��������˽⣬����֧�ֿ�չ��ռ![]() ���ڳ�ȡ����������
���ڳ�ȡ����������![]() ���г�֧��̬�ȵ�Ϊ
���г�֧��̬�ȵ�Ϊ![]() ��.
��.
��1�����![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ�Ա���֧������йأ�
�İ�����Ϊ�Ա���֧������йأ�
֧�� | ��֧�� | �ϼ� | |
���� | |||
�� | |||
�ϼ� |
��2��Ϊ�˽�һ������Կ�չ��ͳ�Ļ�������ͽ��飬�ӳ�ȡ��![]() λ�����жԲ�֧�ֵİ��շֲ�����ķ�����ȡ
λ�����жԲ�֧�ֵİ��շֲ�����ķ�����ȡ![]() λ�����ӳ�ȡ��
λ�����ӳ�ȡ��![]() ���������ѡȡ
���������ѡȡ![]() �˽�����̸����ѡȡ��
�˽�����̸����ѡȡ��![]() ��ǡ��Ϊ
��ǡ��Ϊ![]() ��
��![]() Ů�ĸ���.
Ů�ĸ���.
����
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ��Ȼ�����ĵ���.
Ϊ��Ȼ�����ĵ���.
��1����![]() ʱ��֤����
ʱ��֤����![]() ��
��![]() ��
��
��2��������![]() ��
��![]() �ϴ��ڼ�ֵ�㣬��ʵ��
�ϴ��ڼ�ֵ�㣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A-BCD�У�![]() ����EΪ��CD�ϵ�һ�㣬��
����EΪ��CD�ϵ�һ�㣬��![]() .
.
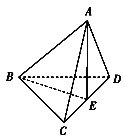
��1����֤:ƽ��![]() ƽ��BCD��
ƽ��BCD��
��2��������A-BCD�����Ϊ![]() ��������E-ABD�ĸ�.
��������E-ABD�ĸ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˵����Уѧ���Ա������ߵĹ�ϵ���Ը�У1000��ѧ������![]() �ı������г������飬�õ�����Ƶ���ֲ������£�
�ı������г������飬�õ�����Ƶ���ֲ������£�
��������Ƶ�ʷֲ���
�������� ����λ�����ף� |
|
|
|
|
|
|
Ƶ�� | 7 | 10 | 19 | 18 | 4 | 2 |
Ů������Ƶ���ֲ���
Ů������ ����λ�����ף� |
|
|
|
|
|
|
Ƶ�� | 3 | 10 | 15 | 6 | 3 | 3 |
��1��������1000��ѧ����Ů����������
��2��������1000��ѧ����������![]() �ĸ��ʣ�
�ĸ��ʣ�
��3���������У���������![]() ��Ů������ȡ2��Ů�����е��飬����2��ѧ��������
��Ů������ȡ2��Ů�����е��飬����2��ѧ��������![]() �ĸ���.�����ߵ�λ�����ף�
�ĸ���.�����ߵ�λ�����ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com