
【题目】抛物线![]() 的焦点F为圆C:
的焦点F为圆C:![]() 的圆心.
的圆心.
![]() 求抛物线的方程与其准线方程;
求抛物线的方程与其准线方程;
![]() 直线l与圆C相切,交抛物线于A,B两点;
直线l与圆C相切,交抛物线于A,B两点;
![]() 若线段AB中点的纵坐标为
若线段AB中点的纵坐标为![]() ,求直线l的方程;
,求直线l的方程;
![]() 求
求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;②
;②![]()
【解析】
(1)由圆C:![]() 配方可得:
配方可得:![]() ,可得圆心
,可得圆心![]() 可得抛物线的焦点
可得抛物线的焦点![]() 因此
因此![]() ,解得
,解得![]() ,即可得出.
,即可得出.
(2)设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() 由直线
由直线![]() 与圆
与圆![]() 相切,可得:
相切,可得:![]() ,或
,或![]() 直线与抛物线联立,化为:
直线与抛物线联立,化为:![]() ,
,![]() 进而得到
进而得到![]() ,或
,或![]() ,根与系数的关系可得
,根与系数的关系可得![]() ,
,![]() ,
,![]() 根据中点坐标公式即可求出m的值,可得直线方程,
根据中点坐标公式即可求出m的值,可得直线方程,![]() 利用数量积运算性质,再利用二次函数的单调性即可得出.
利用数量积运算性质,再利用二次函数的单调性即可得出.
解:(1)由圆![]()
![]() 配方可得:
配方可得:![]() ,可得圆心
,可得圆心![]() .
.
![]() 抛物线的焦点
抛物线的焦点![]() .
.
![]() ,解得
,解得![]() .
.
![]() 抛物线的准线方程为:
抛物线的准线方程为:![]() .
.
![]() 抛物线的方程为
抛物线的方程为![]()
(2)设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
![]() 直线
直线![]() 与圆
与圆![]() 相切,
相切,
![]() ,化为:
,化为:![]() .
.
![]() ,或
,或![]() .
.
联立![]() ,化为:
,化为:![]() ,
,
![]() .
.
![]() ,或
,或![]() .
.
即![]() ,解得
,解得![]() 或
或![]()
所以可得![]() 的范围为
的范围为![]() 或
或![]()
![]() ,
,![]() .
.
![]() 线段
线段![]() 中点的纵坐标为
中点的纵坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]()
②![]()
![]()
![]()
![]()
![]()
![]() .
.
设![]()
![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() 单调递增,
单调递增,![]() ,
,
当![]() 时,
时,![]() 单调递减,
单调递减,![]()
![]() .
.
![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校开展主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据以下信息,解答下列问题:
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 |
| 40% |
合格 | 6 |
|
待合格 | 3 | 6% |
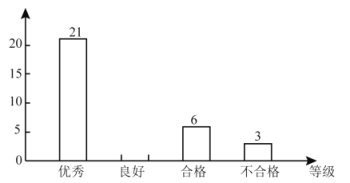
(1)本次调查随机抽取了__________名学生,表中![]() __________,
__________,![]() __________;
__________;
(2)补全条形统计图;
(3)若全校有![]() 名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
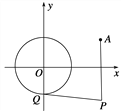
(1)求a,b间的关系;
(2)求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某工厂生产的一种产品的尺寸是否合格,现从500件产品中抽出10件进行检验先将500件产品编号为000,001,002,![]() ,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读
,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读![]() 为了便于说明,下面摘取了随机数表,附表1的第6行至第8行
为了便于说明,下面摘取了随机数表,附表1的第6行至第8行![]() ,即第一个号码为439,则选出的第4个号码是( )
,即第一个号码为439,则选出的第4个号码是( )
162277943949544354821737932378
844217533157245506887704744767
630163785916955567199810507175
A.548B.443C.379D.217
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用![]() ,
,![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为![]() 和
和![]() 之差的绝对值,求随机变量X的分布列与数学期望
之差的绝对值,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)试用“五点法”画出函数![]() 在区间
在区间![]() 的简图;
的简图;
(2)指出该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(3)若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,试求出函数
,试求出函数![]() 的最大值并指出
的最大值并指出![]() 取何值时,函数
取何值时,函数![]() 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com