
【题目】为了调查某工厂生产的一种产品的尺寸是否合格,现从500件产品中抽出10件进行检验先将500件产品编号为000,001,002,![]() ,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读
,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读![]() 为了便于说明,下面摘取了随机数表,附表1的第6行至第8行
为了便于说明,下面摘取了随机数表,附表1的第6行至第8行![]() ,即第一个号码为439,则选出的第4个号码是( )
,即第一个号码为439,则选出的第4个号码是( )
162277943949544354821737932378
844217533157245506887704744767
630163785916955567199810507175
A.548B.443C.379D.217
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为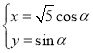 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点F为圆C:
的焦点F为圆C:![]() 的圆心.
的圆心.
![]() 求抛物线的方程与其准线方程;
求抛物线的方程与其准线方程;
![]() 直线l与圆C相切,交抛物线于A,B两点;
直线l与圆C相切,交抛物线于A,B两点;
![]() 若线段AB中点的纵坐标为
若线段AB中点的纵坐标为![]() ,求直线l的方程;
,求直线l的方程;
![]() 求
求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,写出函数
时,写出函数![]() 的单调区间;(直接写出答案,不必写出证明过程)
的单调区间;(直接写出答案,不必写出证明过程)
(2)当![]() 时,求函数
时,求函数![]() 的零点;
的零点;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是![]() ,乙班三名同学答对的概率分别是
,乙班三名同学答对的概率分别是![]() ,
,![]() ,
,![]() ,且这六名同学答题正确与否相互之间没有影响.
,且这六名同学答题正确与否相互之间没有影响.
(1)记“甲、乙两班总得分之和是60分”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示甲班总得分,求随机变量
表示甲班总得分,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值![]() 单位:分
单位:分![]() 对应如下表:
对应如下表:
工人序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
理论成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
实践能力值 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
(1)求这7名工人的理论成绩![]() 与实践能力值
与实践能力值![]() 的中位数、极差;
的中位数、极差;
(2)若规定85分以上![]() 包括85分
包括85分![]() 为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
(3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.![]() 系数精确到
系数精确到![]()
附:线性回归方程![]() 中,
中,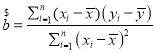 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产了一批高精尖的仪器,为确保仪器的可靠性,工厂安排了一批专家检测仪器的可靠性,毎台仪器被毎位专家评议为“可靠”的概率均为![]() ,且每台仪器是否可靠相互独立.
,且每台仪器是否可靠相互独立.
(1)当![]() ,现抽取4台仪器,安排一位专家进行检测,记检测结果可靠的仪器台数为
,现抽取4台仪器,安排一位专家进行检测,记检测结果可靠的仪器台数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)为进一步提高出厂仪器的可靠性,工厂决定每台仪器都由三位专家进行检测,只有三位专家都检验仪器可靠,则仪器通过检测.若三位专家检测结果都为不可靠,则仪器报废.其余情况,仪器需要回厂返修.拟定每台仪器检测费用为100元,若回厂返修,每台仪器还需要额外花费300元的维修费.现以此方案实施,且抽检仪器为100台,工厂预算3.3万元用于检测和维修,问费用是否有可能会超过预算?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对2019年“双十—”网上购物消费情况,规定:双十一当天购物消费金额不低于600元的网购者为“剁手党”,低于600元的网购者为“理智消费者”.某兴趣小组对双十一当天网购者随机抽取了100名进行抽样分析,得到如下统计图表(单位:人):
女性 | 男性 | 总计 | |
剁手党 | 50 | 5 | 55 |
理智购物者 | 30 | 15 | 45 |
总计 | 80 | 20 | 100 |
(1)根据以上统计数据回答能否在犯错误的概率不超过0.010的前提下认为“剁手党”与性别有关?
(2)现从抽取的80名女性网购者中按照分层抽样的方法选出8人,然后从选出8人中随机选出3人进行调查,选出的剁手党人数为2时的概率.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com