
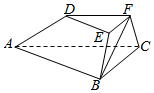
 如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,
如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,分析 (I)先证明BF⊥AC,再证明BF⊥CK,进而得到BF⊥平面ACFD.
(II)方法一:先找二面角B-AD-F的平面角,再在Rt△BQF中计算,即可得出;
方法二:通过建立空间直角坐标系,分别计算平面ACK与平面ABK的法向量,进而可得二面角B-AD-F的平面角的余弦值.
解答 (I)证明:延长AD,BE,CF相交于点K,如图所示,∵平面BCFE⊥平面ABC,∠ACB=90°,
∴AC⊥平面BCK,∴BF⊥AC.
又EF∥BC,BE=EF=FC=1,BC=2,∴△BCK为等边三角形,且F为CK的中点,则BF⊥CK,
∴BF⊥平面ACFD.
(II)方法一:过点F作FQ⊥AK,连接BQ,∵BF⊥平面ACFD.∴BF⊥AK,则AK⊥平面BQF,
∴BQ⊥AK.∴∠BQF是二面角B-AD-F的平面角.
在Rt△ACK中,AC=3,CK=2,可得FQ=$\frac{2\sqrt{13}}{13}$.
在Rt△BQF中,BF=$\sqrt{3}$,FQ=$\frac{2\sqrt{13}}{13}$.可得:cos∠BQF=$\frac{\sqrt{3}}{4}$.
∴二面角B-AD-F的平面角的余弦值为$\frac{\sqrt{3}}{4}$.
方法二:如图,延长AD,BE,CF相交于点K,则△BCK为等边三角形,
取BC的中点,则KO⊥BC,又平面BCFE⊥平面ABC,∴KO⊥平面BAC,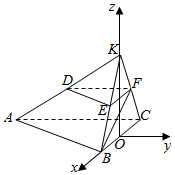
以点O为原点,分别以OB,OK的方向为x,z的正方向,建立空间直角坐标系O-xyz.
可得:B(1,0,0),C(-1,0,0),K(0,0,$\sqrt{3}$),A(-1,-3,0),$E(\frac{1}{2},0,\frac{\sqrt{3}}{2})$,$F(-\frac{1}{2},0,\frac{\sqrt{3}}{2})$.
$\overrightarrow{AC}$=(0,3,0),$\overrightarrow{AK}$=$(1,3,\sqrt{3})$,
$\overrightarrow{AB}$=(2,3,0).
设平面ACK的法向量为$\overrightarrow{m}$=(x1,y1,z1),平面ABK的法向量为$\overrightarrow{n}$=(x2,y2,z2),由$\left\{\begin{array}{l}{\overrightarrow{AC}•\overrightarrow{m}=0}\\{\overrightarrow{AK}•\overrightarrow{m}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{3{y}_{1}=0}\\{{x}_{1}+3{y}_{1}+\sqrt{3}{z}_{1}=0}\end{array}\right.$,
取$\overrightarrow{m}$=$(\sqrt{3},0,-1)$.
由$\left\{\begin{array}{l}{\overrightarrow{AB}•\overrightarrow{n}=0}\\{\overrightarrow{AK}•\overrightarrow{n}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{2{x}_{2}+3{y}_{2}=0}\\{{x}_{2}+3{y}_{2}+\sqrt{3}{z}_{2}=0}\end{array}\right.$,取$\overrightarrow{n}$=$(3,-2,\sqrt{3})$.
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{4}$.
∴二面角B-AD-F的余弦值为$\frac{\sqrt{3}}{4}$.
点评 本题考查了空间位置关系、法向量的应用、空间角,考查了空间想象能力、推理能力与计算能力,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
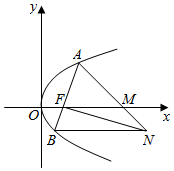 如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1,
如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com