
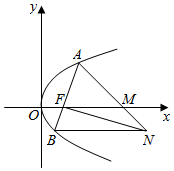
 如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1,
如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1,分析 (Ⅰ)利用抛物线的性质和已知条件求出抛物线方程,进一步求得p值;
(Ⅱ)设出直线AF的方程,与抛物线联立,求出B的坐标,求出直线AB,FN的斜率,从而求出直线BN的方程,根据A、M、N三点共线,可求出M的横坐标的表达式,从而求出m的取值范围.
解答 解:(Ⅰ)由题意可得,抛物线上点A到焦点F的距离等于A到直线x=-1的距离,
由抛物线定义得,$\frac{p}{2}=1$,即p=2;
(Ⅱ)由(Ⅰ)得,抛物线方程为y2=4x,F(1,0),可设(t2,2t),t≠0,t≠±1,
∵AF不垂直y轴,
∴设直线AF:x=sy+1(s≠0),
联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=sy+1}\end{array}\right.$,得y2-4sy-4=0.
y1y2=-4,
∴B($\frac{1}{{t}^{2}},-\frac{2}{t}$),
又直线AB的斜率为$\frac{2t}{{t}^{2}-1}$,故直线FN的斜率为$\frac{{t}^{2}-1}{2t}$,
从而得FN:$y=-\frac{{t}^{2}-1}{2t}(x-1)$,直线BN:y=-$\frac{2}{t}$,
则N($\frac{{t}^{2}+3}{{t}^{2}-1},-\frac{2}{t}$),
设M(m,0),由A、M、N三点共线,得$\frac{2t}{{t}^{2}-m}=\frac{2t+\frac{2}{t}}{{t}^{2}-\frac{{t}^{2}+3}{{t}^{2}-1}}$,
于是m=$\frac{2{t}^{2}}{{t}^{2}-1}$=$\frac{2}{1-\frac{1}{{t}^{2}}}$,得m<0或m>2.
经检验,m<0或m>2满足题意.
∴点M的横坐标的取值范围为(-∞,0)∪(2,+∞).
点评 本题考查抛物线的简单性质,考查直线与圆锥曲线位置关系的应用,考查数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
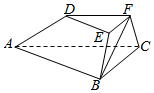 如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,
如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(ex)=|x| | B. | f(ex)=e2x | C. | f(lnx)=lnx2 | D. | f(lnx)=x+$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com