
分析 由AB为圆O:(x-1)2+y2=1的直径,可设A(1+cosθ,sinθ),B(1-cosθ,-sinθ).点P为直线x-y+1=0上任意一点,可设P(x,x+1).利用数量积运算性质、二次函数的单调性即可得出.
解答 解:由AB为圆O:(x-1)2+y2=1的直径,
可设A(1+cosθ,sinθ),B(1-cosθ,-sinθ).
∵点P为直线x-y+1=0上任意一点,可设P(x,x+1),
则$\overrightarrow{PA}$•$\overrightarrow{PB}$=(1+cosθ-x,sinθ-x-1)•(1-cosθ-x,-sinθ-x-1)=(1-x)2-cos2θ+(1+x)2-sin2θ=2x2+1≥1.
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为1,此时P(0,1).
故答案为:1.
点评 本题考查了圆的标准方程、数量积运算性质、二次函数的单调性、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
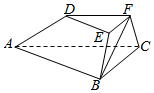 如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,
如图,在三棱台ABC-DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 得病 | 不得病 | 合计 | |
| 干净水 | 52 | 466 | 518 |
| 不干净水 | 94 | 218 | 312 |
| 合计 | 146 | 684 | 830 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com