
分析 无穷等比数列{an}的各项和为A,前n项和为Sn,公比为q,0<|q|≤1,q≠1.可得A=$\frac{{a}_{1}}{1-q}$,Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,由题意可得:an=k(A-Sn),代入化为:k=$\frac{q(1-q)}{{q}^{n}}$,分类讨论即可得出.
解答 解:无穷等比数列{an}的各项和为A,前n项和为Sn,公比为q,0<|q|≤1,q≠1.
则A=$\frac{{a}_{1}}{1-q}$,Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,
由题意可得:an=k(A-Sn),
∴a1q=k($\frac{{a}_{1}}{1-q}$-$\frac{{a}_{1}(1-{q}^{n})}{1-q}$),
化为:k=$\frac{q(1-q)}{{q}^{n}}$,
1>q>0时,k>0,n→+∞时,k→+∞.
-1≤q<0时,可得:n为偶数时,k∈(-∞,-2];n为奇数时,k>0.
∴k∈(-∞,-2]∪(0,+∞).
综上可得:k∈(-∞,-2]∪(0,+∞).
故答案为:(-∞,-2]∪(0,+∞).
点评 本题考查了等比数列的通项公式及其性质、极限性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
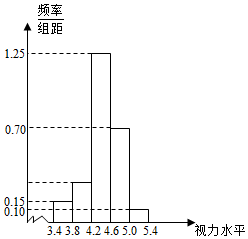 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是4,则根据图中数据可得样本数据在[3.8,4.2)内的人数是12.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是4,则根据图中数据可得样本数据在[3.8,4.2)内的人数是12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-x2+1 | C. | y=lg|x| | D. | y=3x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com