
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{8}$ |
分析 先求出满足向量|$\overrightarrow{a}$|≤2的轨迹,然后利用几何概型的公式去求概率.
解答 解:由题意知m,n∈[0,2],
故点M对应的基本事件Ω是一个边长为2的正方形,所以它的面积为4.
记向量|$\overrightarrow{a}$|≤2对应的事件为P,因为向量|$\overrightarrow{a}$|≤2,得m2+n2≤4,
即事件P对应的基本事件空间是以坐标原点为圆心,半径为2的圆在第一象限内的部分,其面积为π,
即|$\overrightarrow{a}$|≤2的概率是$\frac{π}{4}$.
故选:B.
点评 本题的考点是与面积有关几何概型,首先利用条件将事件转化为对应的平面图形是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 一条线段与一段劣弧 | B. | 一条射线与一段劣弧 | ||
| C. | 一条射线与半圆 | D. | 一条直线和一个圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
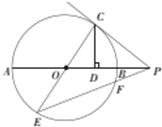 如图,点C为圆O上一点,CP为圆的切线,CE为圆的直径,CP=3.
如图,点C为圆O上一点,CP为圆的切线,CE为圆的直径,CP=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 12 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [7,8] | B. | [0,8] | C. | [$\frac{11}{2}$,8] | D. | [$\frac{11}{2}$,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com