
【题目】如图,四边形![]() 为菱形,四边形
为菱形,四边形![]() 为平行四边形,设
为平行四边形,设![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() .
.
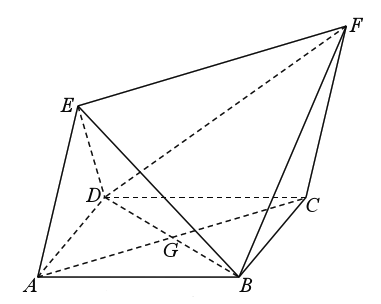
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成角为60°,求二面角
所成角为60°,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根(1)要证面面垂直,需要找线面垂直,本题中重点分析线段![]() ,利用条件底面是菱形可得
,利用条件底面是菱形可得![]() ,通过全等可知
,通过全等可知![]() ,从而
,从而![]() ,故
,故![]() 是平面
是平面![]() 的垂线,从而得证;(2)涉及二面角的计算,一般需要建系设点,计算平面的法向量,利用二面角与法向量夹角之间的关系处理,需要注意建系时分析清楚哪三条线互相垂直.
的垂线,从而得证;(2)涉及二面角的计算,一般需要建系设点,计算平面的法向量,利用二面角与法向量夹角之间的关系处理,需要注意建系时分析清楚哪三条线互相垂直.
试题解析:
(1)证明:连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∵![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(2)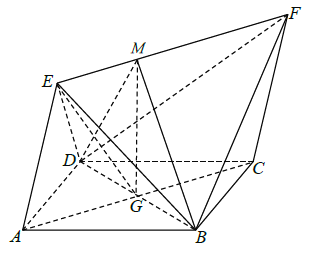
解法一:过![]() 作
作![]() 垂线,垂足为
垂线,垂足为![]() ,连接
,连接![]() ,易得
,易得![]() 为
为![]() 与面
与面![]() 所成的角,
所成的角,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角,
的平面角,
可求得![]() ,
,
在![]() 中由余弦定理可得:
中由余弦定理可得: ![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() ;
;
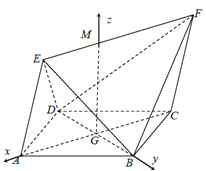
解法二:如图,在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 于
于![]() 点,由(1)可知,平面
点,由(1)可知,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴直线![]() 两两互相垂直,
两两互相垂直,
分别![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
易得![]() 为
为![]() 与平面
与平面![]() 所成的角,∴
所成的角,∴![]() ,
,
则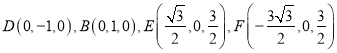 ,
,
 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
![]() 且
且![]() ,
,
∴![]() ,且
,且![]()
取![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
同理可求得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时![]() 千米的速度匀速行驶
千米的速度匀速行驶![]() 千米(
千米(![]() ).假设汽油的价格是每升
).假设汽油的价格是每升![]() 元,而汽车每小时耗油
元,而汽车每小时耗油 升,司机的工资是每小时
升,司机的工资是每小时![]() 元.
元.
(1)求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2)当![]() 为何值时,这次行车的总费用最低?并求出最低费用的值.
为何值时,这次行车的总费用最低?并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.单位向量都相等
B.若 ![]() 与
与 ![]() 是共线向量,
是共线向量, ![]() 与
与 ![]() 是共线向量,则
是共线向量,则 ![]() 与
与 ![]() 是共线向量
是共线向量
C.| ![]() +
+ ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]()
![]() =0
=0
D.若 ![]() 与
与 ![]() 是单位向量,则
是单位向量,则 ![]()
![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com