
分析 (1)当a=2时,将函数f(x)变形,然后利用均值不等式即可求出函数f(x)的最小值;
(2)先取值任取0≤x1<x2然后作差f(x1)-f(x2),判定其符号即可判定函数f(x)在[0,+∞)上的单调性,从而求出函数的最小值.
解答 解:(1)当a=2时,f(x)=x+$\frac{2}{x+1}$=x+1+$\frac{2}{x+1}$-1≥2$\sqrt{2}$-1
当且仅当x+1=$\frac{2}{x+1}$,即x=$\sqrt{2}$-1时取等号,
∴f(x)min=2$\sqrt{2}$-1.
(2)当0<a<1时,任取0≤x1<x2,
f(x1)-f(x2)=(x1-x2)[1-$\frac{a}{{(x}_{1}+1){(x}_{2}+1)}$],
∵0<a<1,(x1+1)(x2+1)>1,
∴1-$\frac{a}{{(x}_{1}+1){(x}_{2}+1)}$>0,
∵x1<x2,∴f(x1)<f(x2),即f(x)在[0,+∞)上为增函数,
∴f(x)min=f(0)=a.
点评 本题主要考查了函数的最值的求解,以及函数单调性的判断与证明,同时考查了计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
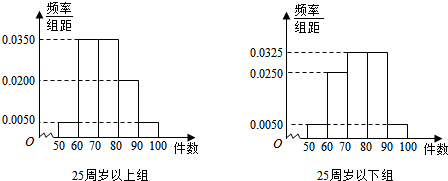
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
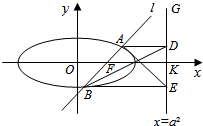 如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{n}^{9}$x9 | B. | C${\;}_{n}^{8}$x8 | C. | C${\;}_{n}^{9}$xn-9 | D. | C${\;}_{n}^{8}$xn-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
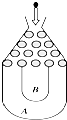 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com