
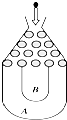
 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.分析 (I)确定事件记“小球落入A袋中”为事件M,“小球落入B袋中”为事件N,则事件M的对立事件为事件N.得出P(M)=P3+(1-P)3=P3+1-3P+3P2-P3=3(P-$\frac{1}{2}$)2$+\frac{1}{4}$,利用函数式子求解即可.
(II)P(M)=($\frac{1}{3}$)3+($\frac{2}{3}$)3=$\frac{1}{27}$$+\frac{8}{27}$=$\frac{1}{3}$.P(N)=1-P(M)=1-$\frac{1}{3}$=$\frac{2}{3}$.利用服从ξ~B(4,$\frac{2}{3}$),数学期望公式即可.
解答 解:(Ⅰ)记“小球落入A袋中”为事件M,“小球落入B袋中”为事件N,则事件M的对立事件为事件N.
而小球落入A袋中当且仅当小球一直向左落下或一直向右落下,
故P(M)=P3+(1-P)3=P3+1-3P+3P2-P3=3(P-$\frac{1}{2}$)2$+\frac{1}{4}$,
∴当P=$\frac{1}{2}$时,P(M)取最小值$\frac{1}{4}$,P(N)取最大值1-$\frac{1}{4}$=$\frac{3}{4}$.
(Ⅱ)由(Ⅰ)知当P=$\frac{1}{3}$时,
随机变量ξ的所有可能取值为0,1,2,3,4.且ξ~B(4,$\frac{2}{3}$),
∴E(ξ)=4×$\frac{2}{3}$=$\frac{8}{3}$.
点评 本题考察了学生的实际应用问题,;离散型的概率求解,重复试验的数学期望公式的运用,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相切或相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$f($\frac{π}{12}$)<f($\frac{π}{6}$) | B. | f($\frac{1}{4}$)$>2f(\frac{π}{12})$sin$\frac{1}{2}$ | C. | $\sqrt{3}$f($\frac{π}{8}$)>$\sqrt{2}$f($\frac{π}{6}$) | D. | $\sqrt{2}$f($\frac{π}{12}$)>f($\frac{π}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com