
分析 (1)通过$\frac{1}{{a}_{1}}$,$\frac{1}{{a}_{2}}$,$\frac{1}{{a}_{4}}$成等差数列可得d2=da1,进而可得结论;
(2)通过an=an可得$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{a}$•$\frac{1}{{2}^{n-1}}$,通过错位相减法可知Bn=$\frac{2}{a}$•(2-$\frac{2+n}{{2}^{n}}$),通过Sn=$\frac{an(n+1)}{2}$可得$\frac{1}{{S}_{n}}$=$\frac{2}{a}$($\frac{1}{n}$-$\frac{1}{n+1}$),并项相加即可,进而可得结论.
解答 解:(1)设等差数列{an}的公差为d,
∵$\frac{1}{{a}_{1}}$,$\frac{1}{{a}_{2}}$,$\frac{1}{{a}_{4}}$成等差数列,
∴$(\frac{1}{{a}_{2}})^{2}$=$\frac{1}{{a}_{1}}$•$\frac{1}{{a}_{4}}$,
∴(a1+d)2=a1(a1+3d),
即d2=da1,
又∵d≠0,∴d=a1=a,
∴an=a+a(n-1)=an,
∴Sn=$\frac{n•(a+an)}{2}$=$\frac{an(n+1)}{2}$;
(2)∵an=an,
∴${a}_{{2}^{n-1}}$=a•2n-1,
∴$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{a}$•$\frac{1}{{2}^{n-1}}$,
∴B${\;}_{n}=\frac{1}{{a}_{1}}$$+\frac{2}{{a}_{2}}$$\frac{3}{{a}_{{2}^{2}}}$+…$+\frac{n}{{a}_{{2}^{n-1}}}$
=$\frac{1}{a}$•(1+2•$\frac{1}{{2}^{1}}$+3•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n-1}}$),
∴$\frac{1}{2}$Bn=$\frac{1}{a}$•($\frac{1}{{2}^{1}}$+2•$\frac{1}{{2}^{2}}$+3•$\frac{1}{{2}^{3}}$+…+n•$\frac{1}{{2}^{n}}$),
两式相减得:$\frac{1}{2}$Bn=$\frac{1}{a}$•(1+$\frac{1}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$)
=$\frac{1}{a}$•($\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$)
=$\frac{1}{a}$•(2-$\frac{2+n}{{2}^{n}}$),
∴Bn=$\frac{2}{a}$•(2-$\frac{2+n}{{2}^{n}}$).
∵Sn=$\frac{an(n+1)}{2}$,
∴$\frac{1}{{S}_{n}}$=$\frac{2}{a}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴An=$\frac{1}{{S}_{1}}$$+\frac{1}{{S}_{2}}$$+\frac{1}{{S}_{3}}$$+…+\frac{1}{{S}_{n}}$
=$\frac{2}{a}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=$\frac{2}{a}$(1-$\frac{1}{n+1}$).
∵当n≥2时,1-$\frac{1}{n+1}$<2-$\frac{2+n}{{2}^{n}}$,
∴当a>0时,An<Bn;当a<0时,An>Bn.
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
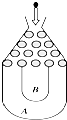 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n-1 | B. | an=2n | C. | an=2n | D. | an=2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com