
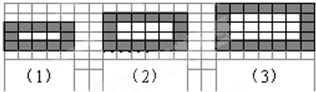
 如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.
如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块. 分析 本题通过观察前几个图案的规律进行归纳,在归纳时要抓住每个情况中反映的数量关系与序号之间的关系再进行概括.
解答 解:根据题目给出的图,我们可以看出:
1图中有黑色瓷砖12块,我们把12可以改写为3×4;
2图中有黑色瓷砖16块,我们把16可以改写为4×4;
3图中有黑色瓷砖20块,我们把20可以改写为5×4;
从具体中,我们要抽象出瓷砖的块数与图形的个数之间的关系,就需要对3、4、5这几个数字进行进一步的变形,用序列号1、2、3来表示,这样12,我们又可以写为12=(1+2)×4,16又可以写为16=(2+2)×4,20我们又可以写为20=(3+2)×4,注意到1、2、3恰好是图形的序列号,而2、4在图中都是确定的,
因此,我们可以从图中概括出第n个图有(n+2)×4,也就是,有4n+8块黑色的瓷砖.
当n=1846时,4n+8=7392,
故答案为:7392
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)及(0,1) | B. | (-1,0)及(1,+∞) | C. | (-1,1) | D. | (-∞,-1)及(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com