
| A. | $\sqrt{3}$f($\frac{π}{12}$)<f($\frac{π}{6}$) | B. | f($\frac{1}{4}$)$>2f(\frac{π}{12})$sin$\frac{1}{2}$ | C. | $\sqrt{3}$f($\frac{π}{8}$)>$\sqrt{2}$f($\frac{π}{6}$) | D. | $\sqrt{2}$f($\frac{π}{12}$)>f($\frac{π}{8}$) |
分析 根据商的关系化简2f(x)<f′(x)tan2x,由式子的特点和求导公式、法则构造函数g(x)=$\frac{f(x)}{sin2x}$,求出g′(x)根据条件判断出符号,得到g(x)的单调性,利用单调性验证出正确答案.
解答 解:∵在(0,$\frac{π}{4}$)上满足2f(x)<f′(x)tan2x,
∴2(cos2x)f(x)<f′(x)sin2x,
设g(x)=$\frac{f(x)}{sin2x}$,则g′(x)=$\frac{f′(x)sin2x-2(cos2x)f(x)}{si{n}^{2}2x}$>0,
∴g(x)在(0,$\frac{π}{4}$)上单调递增,
∴g($\frac{π}{6}$)>g($\frac{π}{12}$),则$\frac{f(\frac{π}{6})}{sin\frac{π}{3}}>\frac{f(\frac{π}{12})}{sin\frac{π}{6}}$,
化简可得$\sqrt{3}f(\frac{π}{12})<f(\frac{π}{6})$,
故选:A.
点评 本题考查求导公式和法则,利用导数研究函数的单调性,以及构造函数法,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
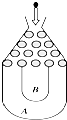 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,有一条长为50$\sqrt{2}$(米)的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为100(米).
如图,有一条长为50$\sqrt{2}$(米)的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为100(米).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com