
某少数民族的刺绣有着悠久的历史,如下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第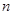 个图形包含
个图形包含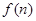 个小正方形.
个小正方形.
(1)求出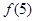 的值;
的值;
(2)利用合情推理的“归纳推理思想”,归纳出 与
与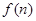 之间的关系式,并根据你得到的关系式求出
之间的关系式,并根据你得到的关系式求出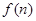 的表达式;
的表达式;
(3)求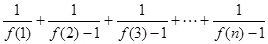 的值.
的值.
解: (1)f(5)=41.
(2)因为f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
……
由上式规律,所以得出f(n+1)-f(n)=4n.
因为f(n+1)-f(n)=4n⇒f(n+1)=f(n)+4n
⇒f(n)=f(n-1)+4(n-1)=f(n-2)+4(n-1)+4(n-2)=f(n-3)+4(n-1)+4(n-2)+4(n-3)
=…=f(1)+4(n-1)+4(n-2)+4(n-3)+…+4=2n2-2n+1.
(3)当n≥2时, =
=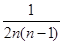 =
=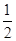 (
(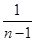 -
-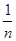 ),
),
∴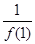 +
+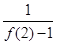 +
+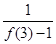 +…+
+…+ =1+
=1+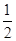 ·(1-
·(1-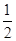 +
+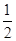 -
- +
+ -
- +…+
+…+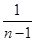 -
-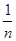 )=1+
)=1+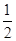 (1-
(1-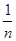 )=
)=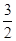 -
-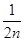 .
.
解析


科目:高中数学 来源: 题型:解答题
(14分)数列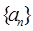 中,
中,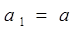 ,
, 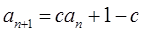
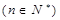
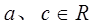
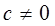
(1)求证: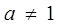 时,
时, 是等比数列,并求
是等比数列,并求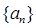 通项公式。
通项公式。
(2)设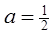 ,
,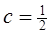 ,
,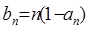
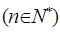 求:数列
求:数列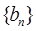 的前n项的和
的前n项的和 。
。
(3)设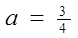 、
、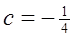 、
、 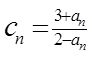 。记
。记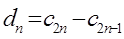 ,数列
,数列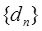 的前n项和
的前n项和 。证明:
。证明: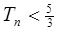
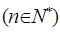 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知数列 中,
中, ,
,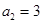 ,其前
,其前 项和
项和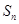 满足
满足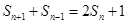 (
(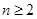 ,
,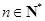 ).
).
(Ⅰ)求证:数列 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)设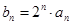 , 求数列
, 求数列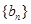 的前
的前 项和
项和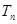 ;
;
(Ⅲ)设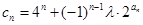 (
(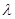 为非零整数,
为非零整数,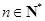 ),试确定
),试确定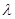 的值,使得对任意
的值,使得对任意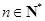 ,有
,有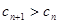 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com