
分析 (1)由a1+2a2+22a3+…+2n-1an=4n,下推一项后,两式相减即可求得其通项an;
(2)n≥2时,利用等比数列的求和公式可求得Sn=4+3×21+3×22+…+3×2n-1=4+3(2n-2),再验证n=1是否适合,即可求得数列{an}的前n项和 Sn.
解答 解:(1)a1+2a2+22a3+…+2n-1an=4n,①
∴a1+2a2+22a3+…+2nan+1=4n+1,②
②-①得2n an+1=3×4n,
∴an+1=3×2n,
又n=1时a1=4,∴综上an=$\left\{\begin{array}{l}4,(n=1)\\ 3×{2^{n-1}},(n≥2)\end{array}\right.$为所求;…(8分)
(2)n≥2时,
Sn=4+3×21+3×22+…+3×2n-1=4+3•$\frac{2(1{-2}^{n-1})}{1-2}$=4+3(2n-2),
又n=1时S1=4也成立,
∴Sn=3×2n-2…(12分)
点评 本题主要考查数列的基础知识,考查分类讨论的数学思想,考查考生综合应用所学知识创造性解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 37 | C. | 58 | D. | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
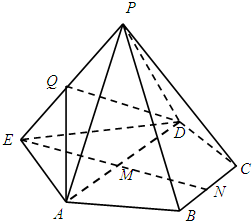 已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE
已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
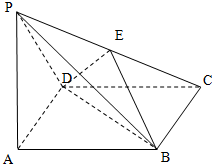 在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com