
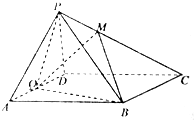
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直.| 1 |
| 3 |
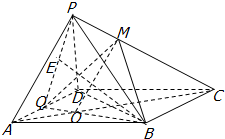 (Ⅰ)证明:连接AC,设AC∩BQ=O,连接OM.
(Ⅰ)证明:连接AC,设AC∩BQ=O,连接OM.| AO |
| OC |
| AQ |
| CB |
| 1 |
| 2 |
| AO |
| AC |
| 1 |
| 3 |
| CO |
| CA |
| CM |
| CP |
| 2 |
| 3 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
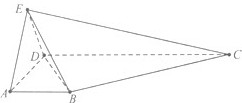 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 按规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间.属酒后驾车:在800mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查处酒后驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间.属酒后驾车:在800mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查处酒后驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
1+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com