
分析 (Ⅰ)利用三种方程的转化方法,即可写出曲线C和直线l2的普通方程;
(Ⅱ)l1的参数方程$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$代入圆C方程、l2的方程,利用参数的几何意义,即可得出结论.
解答 解:(Ⅰ)曲线C:$\left\{\begin{array}{l}{x=-3+4cosθ}\\{y=4+4sinθ}\end{array}\right.$(θ为参数),普通方程为(x+3)2+(y-4)2=16;
l2:cosθ-2sinθ=$\frac{4}{ρ}$普通方程为x-2y-4=0;
(Ⅱ)l1的参数方程$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$代入圆C方程可得t2+4(cosα-2sinα)t-12=0,
t1+t2=-4(cosα-2sinα),
∴|AP|=$\frac{1}{2}$|t1+t2|=|2(cosα-2sinα)|
代入l2的方程,可得t=|AQ|=|$\frac{5}{cosα-2sinα}$|,
∴|AP|•|AQ|=10.
点评 本题考查三种方程的转化,考查参数方程的运用,考查参数的几何意义,属于中档题.


科目:高中数学 来源: 题型:选择题
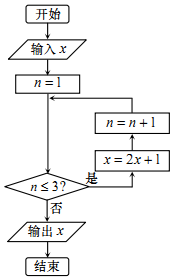 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
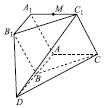 如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.
如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象关于点($\frac{π}{6}$,0)对称 | B. | 函数f(x)的图象关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10步、50步 | B. | 20步、60步 | C. | 30步、70步 | D. | 40步、80步 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com