
分析 先求出基本事件总数n=C76×$\frac{{C}_{6}^{3}{C}_{3}^{3}}{{A}_{2}^{2}}$×A22=140,再求出两天中恰好各有1名女生,包含的基本事件个数m=${C}_{4}^{4}{C}_{3}^{2}×\frac{{C}_{4}^{2}{C}_{2}^{1}}{{A}_{2}^{2}}×{A}_{2}^{2}$=36,由此能求出两天中恰好各有1名女生的概率.
解答 解:先从7人中任取6人,共有C76种不同的取法.
再把6人分成两部分,每部分3人,共有$\frac{{C}_{6}^{3}{C}_{3}^{3}}{{A}_{2}^{2}}$种分法.
最后排在周六和周日两天,有A22种排法,
∴7名志愿者中有3名女生,从其中安排6人在周六、周日两天参加社区公益活动,每天安排3人,
基本事件总数n=C76×$\frac{{C}_{6}^{3}{C}_{3}^{3}}{{A}_{2}^{2}}$×A22=140种.
两天中恰好各有1名女生,包含的基本事件个数:
m=${C}_{4}^{4}{C}_{3}^{2}×\frac{{C}_{4}^{2}{C}_{2}^{1}}{{A}_{2}^{2}}×{A}_{2}^{2}$=36种,
∴两天中恰好各有1名女生的概率p=$\frac{m}{n}$=$\frac{36}{140}$=$\frac{9}{35}$.
故答案为:$\frac{9}{35}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式、排列组合知识的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是
中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是 ,则 8335 用算筹可表示为( )
,则 8335 用算筹可表示为( )| A. |  | B. | 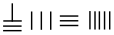 | C. |  | D. | 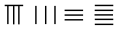 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 略有盈利 | B. | 略有亏损 | ||
| C. | 没有盈利也没有亏损 | D. | 无法判断盈亏情况 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
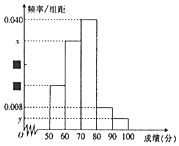 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a |  |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) |  | 0.08 |
| 第5组 | [90,100) | 2 | b |
| 合计 |  |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | y=-x3 | C. | $y=3{x^{\frac{1}{3}}}$ | D. | $y=x+\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分条件 | D. | 必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com