练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

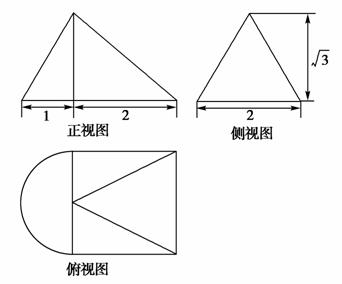
    一个几何体的三视图如图所示，则这个几何体的体积为(　　)


    A

    [解析]　该几何体由底半径为1的半圆锥与四棱锥组成，且高都为，四棱锥底面为正方形，边长为2，因此该几何体体积为V＝·(·π·12)·＋·(2×2)×＝＋＝，故选A.

    6.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知双曲线的中心在原点，焦点F1、F2在坐标轴上，离心率为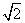，且过点(4，－)．

    (1)求双曲线的方程；

    (2)若点M(3，m)在双曲线上，求证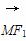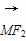：·＝0；

    (3)在(2)的条件下，求△F1MF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


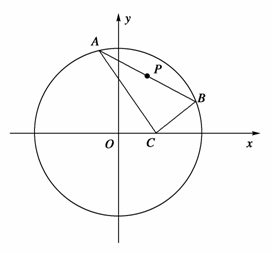
    已知点C(1,0)，点A、B是⊙O：x2＋y2＝9上任意两个不同的点，且满足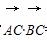＝0，设P为弦AB的中点．

    (1)求点P的轨迹T的方程；

    (2)试探究在轨迹T上是否存在这样的点：它到直线x＝－1的距离恰好等于到点C的距离？若存在，求出这样的点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


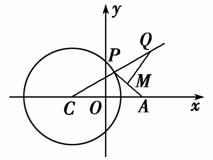
    (2014·鹤壁淇县检测)如图所示，已知C为圆(x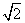＋)2＋y2＝4的圆心，点A(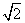，0)，P是圆上的动点，点Q在圆的半径CP所在直线上，且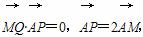当点P在圆上运动时，求点Q的轨迹方程．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个空间几何体的三视图如图所示，则该几何体的表面积为(　　)

    A．48　　　　　　　　　　                          B．32＋8

    C．48＋8                                              D．50

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则其表面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱柱ABC－A′B′C′中，已知AA′⊥平面ABC，AA′＝2，BC＝2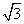，∠BAC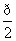＝，且此三棱柱的各个顶点都在一个球面上，则球的体积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


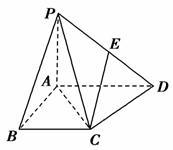
    如图，四棱锥P－ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC＝∠BAD＝90°，PA＝BC＝AD＝1.

    (1)求证：平面PAC⊥平面PCD；

    (2)在棱PD上是否存在一点E，使CE∥平面PAB？若存在，请确定E点的位置；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，正方体ABCD－A1B1C1D1的棱长为2.动点E、F在棱A1B1上，点Q是棱CD的中点，动点P在棱AD上．若EF＝1，DP＝x，A1E＝y(x，y大于零)，则三棱锥P－EFQ的体积(　　)

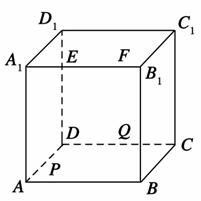
    A．与x、y都有关

    B．与x、y都无关

    C．与x有关，与y无关

    D．与y有关，与x无关

    查看答案和解析>>

    同步练习册答案