Question

13．三棱柱ABC-A₁B₁C₁中，AA₁与AC、AB所成角均为60°，∠BAC=90°，且AB=AC=AA₁=1，则A₁B与AC₁所成角的余弦值为$\frac{\sqrt{3}}{3}$．

Answer 1

分析 由题意画出图形，通过补形得到A₁B与AC₁所成角的补角，求其余弦值后可得A₁B与AC₁所成角的余弦值．

解答 解：如图，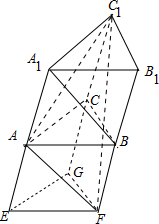
∵AA₁与AC、AB所成角均为60°，AB=AC=AA₁=1，
∴A₁B=1，$A{C}_{1}=\sqrt{{1}^{2}+{1}^{2}-2×1×1×cos120°}$=$\sqrt{3}$，
在三棱柱ABC-A₁B₁C₁下面补上一个完全相同的三棱柱EFG-ABC，
连接C₁F，由题意可得四边形FB₁C₁G为长方形，且$F{B}_{1}=2，{B}_{1}{C}_{1}=\sqrt{2}$，
∴${C}_{1}F=\sqrt{{2}^{2}+（\sqrt{2}）^{2}}=\sqrt{6}$，
在△AFC₁中，$cos∠FA{C}_{1}=\frac{A{F}^{2}+A{{C}_{1}}^{2}-{C}_{1}{F}^{2}}{2AF•A{C}_{1}}$=$\frac{{1}^{2}+（\sqrt{3}）^{2}-（\sqrt{6}）^{2}}{2\sqrt{3}}$=$-\frac{\sqrt{3}}{3}$．
∴A₁B与AC₁所成角的余弦值为$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．

点评 本题考查异面直线及其所成的角，考查学生的空间想象能力和思维能力，是中档题．