
【题目】函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最值;
上的最值;
(2)讨论![]() 的单调性;
的单调性;
(3)当![]() 时,有
时,有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() 在
在![]() 递增;当
递增;当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 上递减.当
上递减.当![]() 时,
时,![]() 在
在![]() 递减.(3)
递减.(3)![]()
【解析】试题分析:(1)![]() 在
在![]() 的最值只能在
的最值只能在![]() 和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数
和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数![]() 在
在![]() 的最值;(2)算出
的最值;(2)算出![]() ,对
,对![]() 的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得
的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∵![]() 的定义域为
的定义域为![]() ,∴由
,∴由![]() ,得
,得![]() .……………………2分
.……………………2分
∴![]() 在区间
在区间![]() 上的最值只可能在
上的最值只可能在![]() 取到,
取到,
而![]() ,
,![]() ,
,![]() ,……4分
,……4分
(2)![]() ,
,![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减;……5分
上单调递减;……5分
②当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增;…………………………6分
上单调递增;…………………………6分
③当![]() 时,由
时,由![]() 得
得![]() ,∴
,∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;……………………8分
上单调递减;……………………8分
综上,当![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
(3)由(2)知,当![]() 时,
时,![]() ,
,
即原不等式等价于![]() ,…………………………12分
,…………………………12分
即![]() ,整理得
,整理得![]() ,
,
∴![]() ,………………13分
,………………13分
又∵![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .……………………14分
.……………………14分


科目:高中数学 来源: 题型:
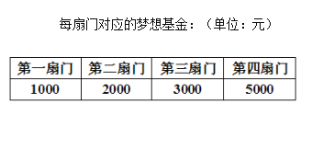
【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对![]() 号
号![]() 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:![]() ;
;![]() (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
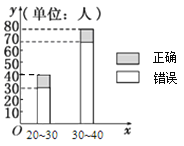
(1)写出![]() 列联表:判断是否有
列联表:判断是否有![]() 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?
说明你的理由.(下面的临界值表供参考)

(2)若某选手能正确回答第一、二、三、四扇门的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是![]() ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考公式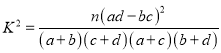 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
, ![]() 是焦点,直线
是焦点,直线![]() 是经过点
是经过点![]() 的任意直线.
的任意直线.
(Ⅰ)若直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 是坐标原点,
是坐标原点, ![]() 是垂足),求动点
是垂足),求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,求证:直线
,求证:直线![]() 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() .
.
(1)设集合![]() 和
和![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数作为
中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率;
上是增函数的概率;
(2)设点![]() 是区域
是区域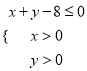 内的随机点,记事件“函数
内的随机点,记事件“函数![]() 有两个零点,其中一个大于1,另一个小于1”为事件
有两个零点,其中一个大于1,另一个小于1”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:设![]() 为每天饮品的销量,
为每天饮品的销量,![]() 为该店每天的利润.
为该店每天的利润.

(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)从日利润不少于96元的几天里任选2天,求选出的这2天日利润都是97元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]()
![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆的右焦点,直线
是椭圆的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(I)求![]() 的方程;
的方程;
(II)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程
的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (其中
(其中![]() 为常数),若函数
为常数),若函数![]() 在区间
在区间![]() 上不存在极值,且存在
上不存在极值,且存在![]() 满
满
足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com