
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【答案】(1)a=2,b=1.(2)![]()
【解析】试题分析:(1)由函数是奇函数可得![]() ,将
,将![]() 代入两个特殊值得到关于
代入两个特殊值得到关于![]() 的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于
的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于![]() 的恒成立不等式,分离参数
的恒成立不等式,分离参数![]() 后通过求函数最值得到
后通过求函数最值得到![]() 的取值范围
的取值范围
试题解析:(1)∵f(x)是奇函数且0∈R,∴f(0)=0即![]()
∴![]()
又由f(1)=-f(-1)知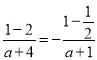
![]() a=2
a=2
∴f(x)=![]()
(2)证明设x1,x2∈(-∞,+∞)且x1<x2
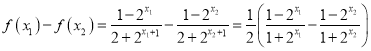
![]() ·
·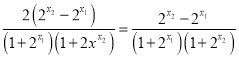
∵y=2x在(-∞,+∞)上为增函数且x1<x2,∴![]()
且y=2x>0恒成立,∴![]()
∴f(x1)-f(x2)>0 即f(x1)>f(x2)
∴f(x)在(-∞,+∞)上为减函数
∵f(x)是奇函数f(x2-x)+f(2x2-t)<0等价于f(x2-x)<-f(2x2-t)=f(-2x2+t)
又∵f(x)是减函数,∴x2-x>-2x2+t
即一切x∈R,3x2-x-t>0恒成立
∴△=1+12t<0,即t<![]()


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)与曲线
为参数)与曲线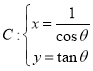 (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 的中点的直角坐标;
的中点的直角坐标;
(2)若直线![]() 的斜率为2,且过已知点
的斜率为2,且过已知点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 有且只有一个极值点,求实数
有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(2)对于函数![]() ,
,![]() ,
,![]() ,若对于区间
,若对于区间![]() 上的任意一个
上的任意一个![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”.已知
上的一个“分界函数”.已知![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得函数
,使得函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”?若存在,求实数
上的一个“分界函数”?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com