
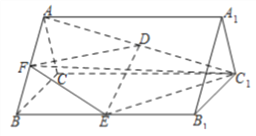
【题目】如图,在正三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.
(1)求证: ![]() //平面
//平面![]() ;
;
(2)若![]() 为
为![]() 中点,求三棱锥
中点,求三棱锥![]() 的体积.
的体积.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: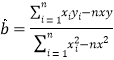 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中![]() 平面
平面![]() ,且
,且![]() ,
,
![]() .
.
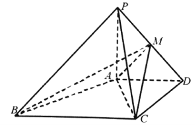
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为45°,如果存在,求
的大小为45°,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:设![]() 为每天饮品的销量,
为每天饮品的销量,![]() 为该店每天的利润.
为该店每天的利润.

(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)从日利润不少于96元的几天里任选2天,求选出的这2天日利润都是97元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为
是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为![]() 平分千米的三角形主题游戏乐园
平分千米的三角形主题游戏乐园![]() ,并在区域
,并在区域![]() 建立水上餐厅.
建立水上餐厅.
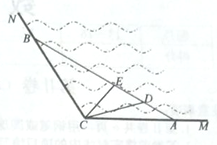
已知![]() ,
, ![]() .
.
(1)设![]() ,
, ![]() ,用
,用![]() 表示
表示![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)设![]() (
(![]() 为锐角),当
为锐角),当![]() 最小时,用
最小时,用![]() 表示区域
表示区域![]() 的面积
的面积![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆市乘坐出租车的收费办法如下:
⑴不超过3千米的里程收费10元; ⑵超过3千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费); 当车程超过3千米时,另收燃油附加费1元. |

相应系统收费的程序框图如图所示,其中![]() (单位:千米)为行驶里程,
(单位:千米)为行驶里程,![]() (单位:元)为所收费用,用
(单位:元)为所收费用,用![]() 表示不大于
表示不大于![]() 的最大整数,则图中①处应填( )
的最大整数,则图中①处应填( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com