
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
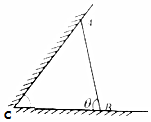 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第3个月 第4个月 | 租用a型车 | 租用b型车 |
| 租用a型车 | 60% | 50% |
| 租用b型车 | 40% | 50% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com