
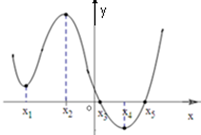
 如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处
如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处分析 通过导函数的图形,直接判断导函数的极值,通过导函数的符号判断函数的极值,写出结果即可.
解答 解:由题意可知(1)导函数y=f′(x)在x2处有极大值.
(2)导函数y=f′(x)在x1、x4处有极小值.
(3)由导函数的图象可知x<x3时,f′(x)>0,函数y=f(x)是增函数,在x∈(x3,x5)时,f′(x)<0,函数y=f(x)是减函数,所以函数f(x)在x3处有极大值.
(4)由于在x∈(x3,x5)时,f′(x)<0,函数y=f(x)是减函数,x>x5时,f′(x)>0,函数y=f(x)是增函数,函数y=f(x)在x5处有极小值.
点评 本题考查函数的极值与导函数的极值的区别与联系,基本知识的考查.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | -$\frac{π}{4}$ | C. | 1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-3=0 | B. | 2x+y=0 | C. | x+y+1=0 | D. | 2x-y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )
函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f(3)-f(2)<f′(2)<f′(3) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f′(3)<f(3)-f(2)<f′(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-e2,$\frac{1}{{e}^{2}}$] | B. | [-e2,$\frac{1}{{e}^{2}}$) | C. | [-e2,$\frac{1}{{e}^{2}}$)∪{$\frac{1}{2e}$} | D. | [-e2,$\frac{1}{{e}^{2}}$)∪{$\frac{2}{3e}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 瓦数 | 94 | 96 | 98 | 100 | 102 | 104 | 106 |
| 甲厂个数 | 0 | 3 | 6 | 8 | 2 | 0 | 1 |
| 乙厂个数 | 1 | 2 | 7 | 4 | 3 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com