
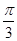 ,且△PF1F2的面积为2
,且△PF1F2的面积为2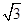 ,双曲线的离心率为2,求该双曲线的标准方程.
,双曲线的离心率为2,求该双曲线的标准方程.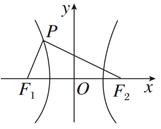
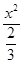 -
-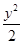 =1
=1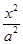 -
-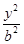 =1(a>0,b>0),则F1(-c,0),F2(c,0),在△PF1F2中,由余弦定理可得
=1(a>0,b>0),则F1(-c,0),F2(c,0),在△PF1F2中,由余弦定理可得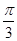 =(|PF1|-|PF2|)2+|PF1|·|PF2|,∴4c2=4a2+|PF1|·|PF2|.
=(|PF1|-|PF2|)2+|PF1|·|PF2|,∴4c2=4a2+|PF1|·|PF2|.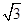 ,∴
,∴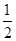 |PF1|·|PF2|·sin
|PF1|·|PF2|·sin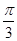 =2
=2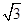 .
.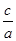 =2,∴c=2a,∴4a2=a2+2,∴a2=.
=2,∴c=2a,∴4a2=a2+2,∴a2=.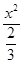 -
-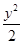 =1.
=1.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
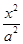 -
-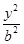 =1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )A.(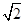 ,+∞) ,+∞) | B.[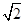 ,+∞) ,+∞) |
C.(1,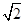 ] ] | D.(1,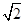 ) ) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
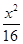 -
-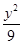 =1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.
=1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
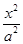 -
- =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )A.-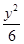 =1 =1 | B.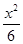 - -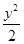 =1 =1 |
C.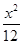 - -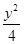 =1 =1 | D.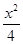 - -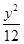 =1 =1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com